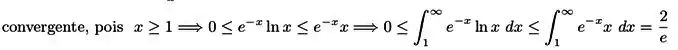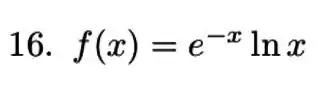
Passo 1
Precisamos determinar a convergência da integral imprópria
Pra que fique mais fácil identificar se essa integral converge podemos utilizar o método da comparação.
Passo 2
Já que neste caso . Temos
Então, se aplicarmos a integral
Passo 3
Sabemos que para resolver uma integral imprópria basta aplicar o limite com
E agora resolvemos normalmente a integral
Para isso podemos utilizar o método da integração por partes. Lembrando la do macete do LIATE, sabemos que:
e
Aplicando na integral por partes
E aplicando os limites ficamos com
Voltando para o limite
Ficamos com
Passo 4
Bom, se
E
Ou seja, converge. Então nossa integral converge!
Resposta
Exercícios de Livros Relacionados
Calcule:int_1^(+ oo) (1)/(sqrt(x)) d x
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 2 π ∞ s e nxd x
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.
Estime o valor numérico de ∫ 0 ∞ e - x 2 d x escrevendo a integral como uma soma de ∫ 0 4 e - x 2 d x e ∫ 4 ∞ e - x 2 d x . Aproxime a primeira integral usando a Regra de Simpson com n = 8 e mostre qu