Avalie as integrais:
a)
b)
c)
d)
e)
f)
g)
Passo 1
Fala galerinha, beleza? Bora resolver umas integrais 😊
No item (a), temos uma integral que sai rapidinho por substituição. Basta fazer , de modo que
Assim,
Daí, é só voltar para variável original usando :
Passo 2
Já no item (b), temos a seguinte integral:
Antes de fazê-la, vamos dar uma fatorada no termo dentro da raiz:
Observe que os três primeiros termos podem ser juntados:
Logo,
Vamos fazer algumas mudanças de variável. A primeira é
Com isso,
Legal, agora temos uma expressão um pouquinho mais limpa! A próxima etapa é fazer uma substituição trigonométrica:
Portanto,
Desta forma, a integral fica:
Agora a gente precisa fazer a integral da secante. Repare que é exatamente isso que ele pede no item (c). Assim, vamos interromper a resolução do item (b) e voltamos a ela no passo 4.
Passo 3
Como dito no fim do passo 2, vamos dar uma pausa na resolução do item (b) e ver com bastante calma o item (c):
Para fazer essa integral multiplicamos e dividimos por :
Agora chamamos o denominador de e percebemos que
Repare que esse é precisamente o numerador, de modo que
Voltando na variável original:
Passo 4
Agora que sabemos a integral da secante, vamos voltar ao item (b). No passo 2 vimos que
onde e . Já que sabemos a integral da secante, temos que
Todavia, precisamos voltar para a variável original. É fácil perceber que
Como , temos que
Portanto,
Assim,
Passo 5
Depois dessa volta maluca, vamos para o item (d):
Eu sei que você já deve estar pensando em frações parciais. Mas repare que o grau do numerador é maior que o grau do denominador. Desta forma, precisamos fazer a divisão de polinômios:
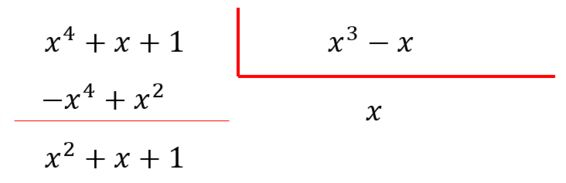
Com isso, podemos escrever:
Assim, temos que
Vamos olhar com atenção para o segundo termo:
Agora partimos para frações parciais:
Comparando termo a termo, construímos o sistema:
Daí, tiramos , de modo que
Somando as equações:
Com isso,
Logo,
Desta forma, quebramos o problema em 4 integrais:
Agora é só integrar e problema resolvido:
Passo 6
Ufa, já foi mais da metade! Bora pro item (e):
Essa integral é resolvida usando integração por partes:
Vamos chamar e , de modo que
Logo,
Para essa integral do lado direito, aplicamos partes novamente com e . Assim,
Com isso,
Mas essa nova integral é exatamente a integral que procuramos e estou chamando de :
Voltando para a relação de antes:
Com isso, passando todos os termos com para o mesmo lado:
Portanto,
Aí é só adicionar a constante e pronto:
Passo 7
Faltam apenas duas! No item (f), a integral é
Você pode tentar fazer essa integral usando relações trigonométricas, dá bastante trabalho, mas sai. Eu gosto de fazer de um jeito diferente usando a fórmula de Euler:
O é o número imaginário mesmo. Repare que
Com isso, podemos escrever
Portanto,
Portanto,
Agora a gente faz a distributiva:
Repare que os termos são exatamente do tipo , de modo que
Viu que legal? Usando a fórmula de Euler nós conseguimos escrever o integrando como uma soma de senos, aí fica fácil integrar:
Fazendo as integrais:
Passo 8
Falta só o item (g) e fechamos o problema! Queremos calcular a integral imprópria
Para isso, lembre-se que essas integrais são limites do tipo:
Desta forma, nosso foca deve ser calcular
Portanto,
Quando , , de modo que esse limite existe:
Portanto,
Aleluia terminamos 😉!