Nos exercícios a discuta a convergência das integrais impróprias.
Passo 1
Bora comparar com o .
Bom, a chave aqui é olha pros limites de integração na hora de comparar. Considerando , temos que
Então:
Logo:
E portanto:
Perceba que nesse caso, colocamos um porque como estamos tratando de logaritmo, não podemos falar , por não existir. Então faremos o limite.
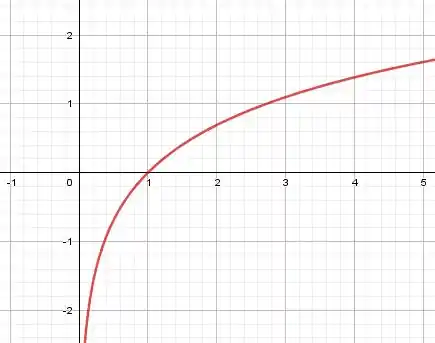
Note, que na função , quanto mais próximo de zero é o , maior ele é e negativo também. Como estamos subtraindo aquele termo, ele fica positivo. Portanto:
Resposta
divergente, pois
Exercícios de Livros Relacionados
Calcule:int_1^(+ oo) (1)/(sqrt(x)) d x
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 2 π ∞ s e nxd x
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.
Estime o valor numérico de ∫ 0 ∞ e - x 2 d x escrevendo a integral como uma soma de ∫ 0 4 e - x 2 d x e ∫ 4 ∞ e - x 2 d x . Aproxime a primeira integral usando a Regra de Simpson com n = 8 e mostre qu