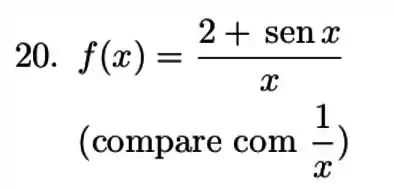
Passo 1
O exercício nos pede para resolver a integral imprópria
Mas como só precisamos avaliar a convergência, podemos fazer isso por comparação. Nos foi recomendado usar
Já que nossos limites estão sempre na condição . Sempre teremos
Então se aplicarmos a integral
Passo 2
Então podemos analisar a convergência observando a integral
Para isso podemos aplicar o limite com .
Para resolver o limite basta integrarmos normalmente
Aplicando os limites de integração
Voltando para o limite
Passo 3
Se sabemos que
E
Ou seja, diverge. Então nossa integral é divergente.
Resposta
Exercícios de Livros Relacionados
Calcule:int_1^(+ oo) (1)/(sqrt(x)) d x
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 2 π ∞ s e nxd x
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.
Estime o valor numérico de ∫ 0 ∞ e - x 2 d x escrevendo a integral como uma soma de ∫ 0 4 e - x 2 d x e ∫ 4 ∞ e - x 2 d x . Aproxime a primeira integral usando a Regra de Simpson com n = 8 e mostre qu