Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Impróprias – Limites Sendo Infinito

Ver Teoria
Exercício 501234567891011121314151617181920212223242526272829303132333435363738394041424344454647484951525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Lista 4.12 - Lista de Integrais – UFSC – Cálculo 1 – Questão 4a

Em cada item, a ∈ R para o qual a integral converge e determine o resultado da integral para esse valor de a .

(a)

∫ 0 ∞ 1 x 2 + 4 - a x + 2 d x

Passo 1

Falaeee, beleza? Vamos colocar uma integral para cada expressão para analisarmos melhor, beleza?

∫ 0 ∞ 1 x 2 + 4 d x + ∫ 0 ∞ a x + 2 d x

Agora vamos resolver cada uma delas, belezinha?

Passo 2

Primeiramente, vamos começar pela menos complicadinha haha:

∫ 0 ∞ a x + 2 d x ∴ lim a → ∞   ⁡ ∫ 0 a a x + 2 d x = a ∙ ln ⁡ | x + 2 |

Passo 3

Agora vamos para a outra integral, belezinha? Vem comigo!!

∫ 0 ∞ 1 x 2 + 4 d x  

Percebemos que trata-se de uma integral a qual será necessária uma substituição trigonométrica. Então se liga:

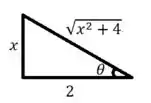
E, comparando com a integral, temos que:

x = 2 tan ⁡ θ ⇒ 4 tan 2 ⁡ θ + 4 ∴ 4 tan 2 ⁡ θ + 1 ∴ 4 sec 2 ⁡ θ = 2 sec ⁡ θ d x = 2 sec 2 ⁡ θ   d θ ∴ θ = arctan ⁡ x 2

Passo 4

Dessa forma, substituindo em ∫ 0 ∞ 1 x 2 + 4 d x  

Temos que:

∫ 0 ∞ 2 sec 2 ⁡ θ 2 sec ⁡ θ d x   = ∫ 0 ∞ 2 sec ⁡ θ d x  

E, resolvendo a integral, temos:

∫ 0 ∞ 2 sec ⁡ θ d x   = lim r → ∞ ⁡ ln ⁡ sec ⁡ θ + tan ⁡ θ r 0 ∴

= lim r → ∞ ⁡ ln ⁡ x 2 + 4 2 + x 2 r 0

Passo 5

Agora, substituindo os resultados das duas integrais, temos:

∫ 0 ∞ 1 x 2 + 4 d x + ∫ 0 ∞ a x + 2 d x = lim r → ∞ ⁡ ln ⁡ x 2 + 4 2 + x 2 r 0 - a ∙ ln ⁡ x + 2 r 0 ∴

= l i m r → ∞ ln ⁡ 1 2 x 2 + 4 + x x + 2 a r 0

Passo 6

Então, se a = 1 , temos que:

= l i m r → ∞ ln ⁡ 1 2 x 2 + 4 + x x + 2 r 0 ∴

= l i m r → ∞ ln ⁡ 1 2 x 1 + 4 x 2 + 1 x 1 + 2 x - l i m r → ∞ ln ⁡ 1 2 x 0 + 4 + 0 0 + 2 ∴

= ln ⁡ 1 - ln ⁡ 1 2 ∴

= ln ⁡ | 2 |

Entendeu direitinho? Responde aee ;)

Resposta

ln ⁡ | 2 |

Exercícios de Livros Relacionados

Calcule:int_1^(+ oo) (1)/(sqrt(x)) d x
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 2 π ∞ s e nxd x
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.
Estime o valor numérico de ∫ 0 ∞ e - x 2 d x escrevendo a integral como uma soma de ∫ 0 4 e - x 2 d x e ∫ 4 ∞ e - x 2 d x . Aproxime a primeira integral usando a Regra de Simpson com n = 8 e mostre qu