Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Impróprias – Limites Sendo Infinito

Ver Teoria
Exercício 221234567891011121314151617181920212324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

4a) Determine se a integral ∫ 0 + ∞ d x x 3 + 5 x 2 + 1 converge ou diverge, justificando sua resposta

Passo 1

Show! Pra começar, vou te dizer que nem precisa se preocupar muito com essa integral doida, vamos pensar numa mais simples:

∫ 0 + ∞ d x x 3

Porque? Bem, olha só, as funções dentro dessa e da outra são bem comparáveis:

1 x 3 + 5 x 2 + 1 < 1 x 3   ,                     x ≥ 0

Se a gente der uma mexidinha, da pra provar essa inequação:

x 3 + 5 x 2 + 1 > x 3

x 3 + 5 x 2 + 1 > x 3

5 x 2 + 1 > 0

5 x 2 > - 1

x 2 > - 1 5

O que é uma verdade já que qualquer número ao quadrado é positivo mesmo! Então tai provado que uma função dessas sempre está acima da outra. Só pra ficar mais visual, saca só os gráficos dessas duas funções:

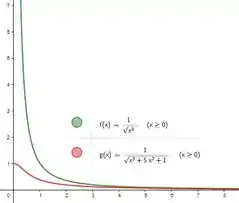
Como a integral pode ser interpretada como a área abaixo do gráfico e 1 x 3 + 5 x 2 + 1 é sempre menor que 1 x 3 , então vamos ter:

∫ 0 + ∞ d x x 3 + 5 x 2 + 1 < ∫ 0 + ∞ d x x 3

Vamos então resolver a integral mais fácil pra ver o que ela nos revela sobre a mais complicada. Mas antes, vamos pensar no seguinte: no limite de integração 0 ! Como as duas funções são contínuas, é justo reescrever a inequação acima para:

∫ 1 + ∞ d x x 3 + 5 x 2 + 1 < ∫ 1 + ∞ d x x 3

Assim a gente nem se preocupa com eventuais divisões por 0 ! Se provarmos que:

∫ 1 + ∞ d x x 3

Converge, provamos que:

∫ 1 + ∞ d x x 3 + 5 x 2 + 1

E logo:

∫ 0 + ∞ d x x 3 + 5 x 2 + 1

Também convergem!

Passo 2

Vamo que vamo. Pra começar, vamos escrever essa integral de uma forma mais conveniente pras contas:

∫ 1 + ∞ d x x 3 = ∫ 1 + ∞ x - 3 2 d x =   lim a → + ∞ ⁡ ∫ 1 a x - 3 2 d x

Fazendo as contitas:

lim a → + ∞ ⁡ x - 1 2 - 1 2 x = 1 x = a = lim a → + ∞ ⁡ - 2 x x = 1 x = a = lim a → + ∞ ⁡ - 2 a + 2 1

lim a → + ∞ ⁡ - 2 a + 2 1 = 0 + 2 = 2

E ta feito! A integral imprópria convergiu! Provamos que:

∫ 0 + ∞ d x x 3 + 5 x 2 + 1   c o n v e r g e !

Resposta

∫ 0 + ∞ d x x 3 + 5 x 2 + 1   c o n v e r g e !

Exercícios de Livros Relacionados

Calcule:int_1^(+ oo) (1)/(sqrt(x)) d x
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 2 π ∞ s e nxd x
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.
Estime o valor numérico de ∫ 0 ∞ e - x 2 d x escrevendo a integral como uma soma de ∫ 0 4 e - x 2 d x e ∫ 4 ∞ e - x 2 d x . Aproxime a primeira integral usando a Regra de Simpson com n = 8 e mostre qu