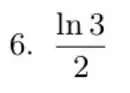Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Impróprias – Limites Sendo Infinito

Ver Teoria
Exercício 741234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727375767778798081828384858687888990919293949596979899100

Enunciado

Nos exercícios 1 a 12 use a definição para verificar se a integral imprópria converge ou diverge. Calcule o valor das integrais impróprias que converge

6 )   ∫ 2 ∞ 1 x 2 - 1 d x

Passo 1

Temos uma integral imprópria já que um dos limites de integração é infinito.

Para saber se a integral converge ou diverge precisamos aplicar o limite da integral e ver se dá um número finito. Se sim, então a integral é convergente. Se ao calcular o limite obtivermos um valor tipo ± ∞ , a integral é divergente.

Passo 2

Quando temos uma integral imprópria desse tipo, precisamos fazer

∫ 2 ∞ 1 x 2 - 1 d x = lim b → ∞ ⁡ ∫ 2 b 1 x 2 - 1 d x ⁡

Passo 3

Agora vamos resolver a integral normalmente. Para isso vamos fatorar o denominador

x 2 - 1 = ( x + 1 ) ( x - 1 )

E dividir em frações parciais

1 x 2 - 1 = A x + 1 + B x - 1

1 x 2 - 1 = A x - 1 ( x + 1 ) ( x - 1 ) + B x + 1 ( x + 1 ) ( x - 1 )

1 = A x - A + B x + B

Logo

- A + B = 1

A + B = 0

E resolvendo, temos:

A = - 1 / 2

B = 1 / 2

Então nossa integral fica

∫ 2 b 1 x 2 - 1 d x = - 1 2 ∫ 2 b 1 x + 1 d x + 1 2 ∫ 2 b 1 x - 1 d x

Resolvendo, ficamos com

∫ 2 b 1 x 2 - 1 d x = - 1 2 ln ⁡ x + 1 + 1 2 ln ⁡ x - 1 2 b

∫ 2 b 1 x 2 - 1 d x = 1 2 ln ⁡ x - 1 x + 1 2 b

Aplicando os limites de integração

∫ 2 b 1 x 2 - 1 d x = 1 2 ln ⁡ b - 1 b + 1 - 1 2 ln ⁡ 2 - 1 2 + 1

Passo 4

Aplicando o limite

∫ 2 ∞ 1 x 2 - 1 d x = lim b → ∞ ⁡ ∫ 2 b 1 x 2 - 1 d x ⁡

∫ 2 ∞ 1 x 2 - 1 d x = lim b → ∞ ⁡ 1 2 ln ⁡ b - 1 b + 1 - 1 2 ln ⁡ 2 - 1 2 + 1       →

∫ 2 ∞ 1 x 2 - 1 d x = lim b → ∞ ⁡ 1 2 ln ⁡ b - 1 b + 1 - 1 2 ln ⁡ 1 3       →

Por propriedade de Limite, o limite da soma é a soma dos limites:

∫ 2 ∞ 1 x 2 - 1 d x = lim b → ∞ ⁡ 1 2 ln ⁡ b - 1 b + 1 + lim b → ∞ ⁡ - 1 2 ln ⁡ 1 3       →

Como o Segundo termo dessa soma aí independe de b (que é quem estamos fazendo ir ao infinito), sai do limite:

∫ 2 ∞ 1 x 2 - 1 d x = lim b → ∞ ⁡ 1 2 ln ⁡ b - 1 b + 1 - 1 2 ln ⁡ 1 3   →

Como nesse limite só tem b na fração, podemos jogar o limite lá dentro:

∫ 2 ∞ 1 x 2 - 1 d x = 1 2 ln ⁡ lim b → ∞ ⁡ b - 1 b + 1 - 1 2 ln ⁡ 1 3  

Passo 5

Calculando o limite:

No limite:

lim b → ∞ ⁡ b - 1 b + 1     →       ∞ ∞

Vemos uma indeterminação, logo, aplicando L’hopital:

lim b → ∞ ⁡ b - 1 b + 1 = lim b → ∞ ⁡ b - 1 ' b + 1 ' =

lim b → ∞ ⁡ 1 1 = 1

Passo 6

Voltando para a integral…

∫ 2 ∞ 1 x 2 - 1 d x = 1 2 ln ⁡ lim b → ∞ ⁡ b - 1 b + 1 - 1 2 ln ⁡ 1 3

Então…

∫ 2 ∞ 1 x 2 - 1 d x = 1 2 ln ⁡ 1 - 1 2 ln ⁡ 1 3   →

∫ 2 ∞ 1 x 2 - 1 d x = - 1 2 ln ⁡ 1 3   →

Como 1 3 = 3 - 1 … E por propriedade logarítimica…

∫ 2 ∞ 1 x 2 - 1 d x = - 1 2 ln ⁡ 3 - 1   →

= ln ⁡ 3 2

O limite resultou em um número finito, logo a integral converge.

Resposta

Exercícios de Livros Relacionados

Calcule:int_1^(+ oo) (1)/(sqrt(x)) d x
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 2 π ∞ s e nxd x
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.
Estime o valor numérico de ∫ 0 ∞ e - x 2 d x escrevendo a integral como uma soma de ∫ 0 4 e - x 2 d x e ∫ 4 ∞ e - x 2 d x . Aproxime a primeira integral usando a Regra de Simpson com n = 8 e mostre qu