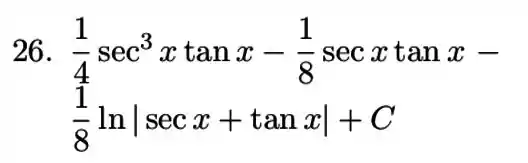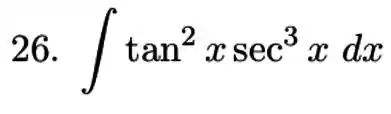
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Trigonométricas

Ver Teoria
Exercício 321234567891011121314151617181920212223242526272829303133343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Essa vai ser grande já se prepara mas vamos entendendo passo a passo.

A primeira coisa é usar a identidade trigonométrica tan 2 ⁡ x = sec 2 x ⁡ - 1 para simplificar nossa expressão.

∫ tan 2 ⁡ x sec 3 ⁡ x   d x = ∫ sec 2 ⁡ x - 1 sec 3 ⁡ x   d x

Com isso podemos dividir nossa integral em duas

∫ tan 2 ⁡ x sec 3 ⁡ x   d x = ∫ sec 5 ⁡ x   d x - ∫ sec 3 ⁡ x   d x

Passo 2

Beleza! Agora vamos resolver a integral

∫ sec 5 ⁡ x   d x = ∫ sec 2 ⁡ x sec 3 ⁡ x   d x

Por partes.

u = sec 3 ⁡ x

d v = sec 2 ⁡ x

Então

d u = 3 tan ⁡ x sec 3 ⁡ x

v = tan ⁡ x

Colocando na formulinha da integral por partes

∫ u d v = u v - ∫ v   d u

∫ sec 5 ⁡ x   d x = sec 3 ⁡ x tan ⁡ x - 3 ∫ tan 2 ⁡ x sec 3 ⁡ x   d x

E podemos fazer de novo a substituição da identidade trigonométrica tan 2 ⁡ x = sec 2 x ⁡ - 1 , então ficamos com

∫ sec 5 ⁡ x   d x = sec 3 ⁡ x tan ⁡ x - 3 ∫ sec 5 ⁡ x   d x + 3 ∫ sec 3 ⁡ x   d x  

Manipulando um pouco mais

∫ sec 5 ⁡ x   d x = 1 4 sec 3 ⁡ x tan ⁡ x + 3 4 ∫ sec 3 ⁡ x   d x

Passo 3

Resolvida essa primeira integral, vamos voltar lá para a nossa expressão do passo 1.

∫ tan 2 ⁡ x sec 3 ⁡ x   d x = ∫ sec 5 ⁡ x   d x - ∫ sec 3 ⁡ x   d x

∫ tan 2 ⁡ x sec 3 ⁡ x   d x = 1 4 sec 3 ⁡ x tan ⁡ x + 3 4 ∫ sec 3 ⁡ x   d x - ∫ sec 3 ⁡ x   d x

∫ tan 2 ⁡ x sec 3 ⁡ x   d x = 1 4 sec 3 ⁡ x tan ⁡ x - 1 4 ∫ sec 3 ⁡ x   d x

Passo 4

Agora falta resolver a integral ∫ sec 3 ⁡ x   d x . De novo vamos usar a integração por partes

∫ sec 3 ⁡ x   d x = ∫ sec 2 ⁡ x sec ⁡ x   d x

u 2 = sec ⁡ x

d v 2 = sec 2 ⁡ x

d u 2 = tan ⁡ x sec ⁡ x

v 2 = tan ⁡ x

Aplicando na formulinha

∫ u 2 d v 2 = u 2 v 2 - ∫ v 2   d u 2

∫ sec 3 ⁡ x   d x = sec ⁡ x tan ⁡ x - ∫ tan 2 ⁡ x sec ⁡ x   d x

E lá vamos nós substituir de novo tan 2 ⁡ x = sec 2 x ⁡ - 1

∫ sec 3 ⁡ x   d x = sec ⁡ x tan ⁡ x - ∫ sec 2 x ⁡ - 1 sec ⁡ x   d x

∫ sec 3 ⁡ x   d x = sec ⁡ x tan ⁡ x - ∫ sec 2 x ⁡ - 1 sec ⁡ x   d x

∫ sec 3 ⁡ x   d x = sec ⁡ x tan ⁡ x - ∫ sec 3 ⁡ x   d x - ∫ sec ⁡ x   d x

Manipulando um pouco

∫ sec 3 ⁡ x   d x = 1 2 sec ⁡ x tan ⁡ x - 1 2 ∫ sec ⁡ x   d x

Passo 5

Voltando para nossa expressão

∫ tan 2 ⁡ x sec 3 ⁡ x   d x = 1 4 sec 3 ⁡ x tan ⁡ x - 1 4 ∫ sec 3 ⁡ x   d x

∫ tan 2 ⁡ x sec 3 ⁡ x   d x = 1 4 sec 3 ⁡ x tan ⁡ x - 1 4 1 2 sec ⁡ x tan ⁡ x + 1 2 ∫ sec ⁡ x   d x

∫ tan 2 ⁡ x sec 3 ⁡ x   d x = 1 4 sec 3 ⁡ x tan ⁡ x - 1 8 sec ⁡ x tan ⁡ x - 1 8 ∫ sec ⁡ x   d x  

Passo 6

Sabemos que a integral

∫ sec ⁡ x   d x   = ln ⁡ tan ⁡ x + sec ⁡ x

Então

∫ tan 2 ⁡ x sec 3 ⁡ x   d x = 1 4 sec 3 ⁡ x tan ⁡ x - 1 8 sec ⁡ x tan ⁡ x - 1 8 ln ⁡ tan ⁡ x + sec ⁡ x + C

Resposta

Exercícios de Livros Relacionados

Deduza uma fórmula similar àquela do Exercício 41 para ∫ cot n ⁡ x d x ,s en for um inteiro positivo maior do que 1.
Calcule a integral. ∫ 0 π 4 sec ⁡ θ tan ⁡ θ d θ
Calcular a área da região limitada por y = tg^3 x , y = 1 e x = 0 .
Calcule a integral.int s e n^2 (pi x) cos^5 ( pi x ) d x
Calcule a integral.int s e n^6 (pi x) d x