UNICAMP. Cálculo 1. 2022.1 – 5º Vespertino. P3. Questão 2b.
Calcule as seguintes integrais:
b)
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nessa questão foi dada uma integral pra a gente calcular em que a função de integração é dada por .
Se a gente for calcular a integral do jeito que a função está vai dar um trabalho enorme então o maior desafio é conseguir visualizar a transformação que temos que fazer pra possibilitar o cálculo dessa integral.
E aí! Tem ideia do que podemos fazer pra facilitar nossa integral?? 🤔🤔
Uma maneira não muito intuitiva e muitas vezes nem um pouco fácil de ser visualizada é o método de substituição de variáveis por funções trigonométricas.
A praticidade desse método é que podemos fazer relações trigonométricas pra simplificar nossa função de integração.
Bora ver como podemos desenvolver esse problema? 😁
Passo 2
Se a gente substituir por , derivando com relação a , temos
Isolando
Substituindo e na integral, vamos obter
Mas o que é ?
Pelas relações trigonométricas, isso é igual a
Fazendo essa substituição na integral, temos
Um número elevado a que está elevado a , por exemplo em , o resultado do expoente em é o produto entre e . no denominador da nossa função de integração é a mesma coisa.
Simplificando essa parte, temos
Substituindo essa informação na integral
Simplificando nossa função, temos
Tranquilo até aqui? 😎
Passo 3
Por fim, qual a relação trigonométrica que podemos fazer com ?
Em alguma parte do ensino médio ou da faculdade já vimos que
Portanto nossa integral final será
Pelo teorema fundamental do cálculo a integral do cosseno é igual ao seno, ou seja
Nesse momento a gente fica topo
Mas se a gente lembrar do triangulo de Pitágoras, temos que a soma do quadrado dos dois catetos resulta na hipotenusa, ou seja com a substituição que fizemos lá no início, temos
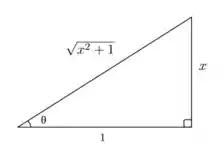
Qual é o seno de um ângulo? O cateto adjacente sobre a hipotenusa, não é? Logo
Logo o resultado da nossa integral será
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
