Nos exercícios de a , resolva a integral indicada. Em alguns casos será preciso aplicar mais de uma técnica de integração.
4)
Passo 1
Bem, se você reparar, a derivada do arco-tangente é justamente dividido por aquele denominador, sugerindo uma integração por partes:
Onde o no nosso caso sempre é quem vamos derivar no caso a arco-tangente, e o é todo resto que vamos integrar, saca?
Passo 2
A segunda tarefa é encontrar o derivando o e o integrando o :
fazendo uma substituição do tipo ...
Voltando para a variável original...
Show de bola! Agora é só trocar na fórmula de integração por partes mesmo:
Passo 3
Bem, o nosso grande problema agora é como encontrar a solução desta integral que é resquício da integração por partes
Você pode ter pensado em fazer uma substituição simples, mas fazer isso não uma boa, afinal quando derivarmos , vai aparecer um e a gente não tem esse lá em cima.
Mas como temos uma soma de com , podemos realizar uma substituição trigonométrica, afinal sabemos que
Olha como o denominador e essa expressão da trigonometria são parecidas! :D Então se substituirmos
e o ...
Logo...
A expressão da secante é...
Então...
Portanto o que temos que fazer agora basicamente é calcular essa integral aí e voltar para a integral original. Bora :D
Passo 4
Para resolver essa integral, como ela é famosinha, recomendo você já ter em mente uma relação muito útil da trigonometria que é
Jogando na integral e trabalhando com o algebrismo da coisa
Substituindo novamente aquele cosseno ao quadrado ali, mas dessa vez lembrando que temos como argumento, então na substituição ele duplica...
Essas integrais já são diretas...
Lembrando que
E que ...
Voltando para a variável original lembrando que , então ... Mas dentro do seno e do cosseno, não vamos trocar pra não ficar feio, mas saiba que essa relação é válida, heim!
Passo 5
Pegando esse resultado individual e voltando para a integração por partes que queríamos laaaaá no passo 2...
Cara! Essa basicamente já é a resposta, mas ela não está nada elegante certo?
O legal é que como arco-tangente é um arco, um ângulo cuja tangente é , podemos descobrir quem é esse seno construindo um triângulo retângulo com a característica de ter a tangente, valendo ... (lembre-se que chamamos de esse arco)
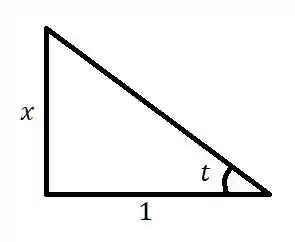
Repare que esse triângulo satisfaz perfeitamente a condição de ou . Completando por Pitágoras...
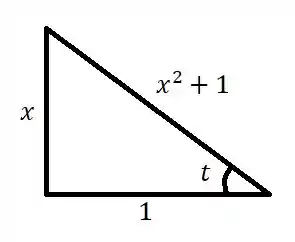
O seno de então é...
Enquanto que o cosseno