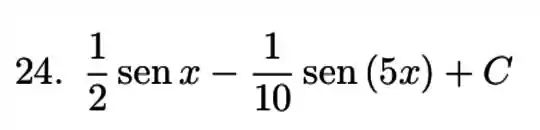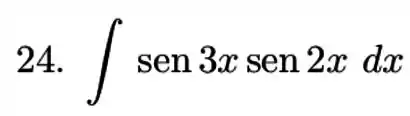
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Trigonométricas

Ver Teoria
Exercício 401234567891011121314151617181920212223242526272829303132333435363738394142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Vamos lá! Para resolver essa questão vamos ter que lembrar lá da soma e subtração de cossenos. Lembra daquelas musiquinhas que a gente decorava para lembrar?

cos ⁡ a + b = cos ⁡ a cos ⁡ b - sen ⁡ a sen ⁡ b

cos ⁡ a - b = cos ⁡ a cos ⁡ b + sen ⁡ a sen ⁡ b

Então, se juntarmos essas equações, vamos chegar em

sen ⁡ a sen ⁡ b = 1 2 cos ⁡ a - b - cos ⁡ a + b

Perceba que nossa integral é um caso desses onde

a = 3 x

b = 2 x

Passo 2

Então agora vamos aplicar a fórmula que chegamos lá em cima na nossa integral

∫ sen ⁡ 3 x sen ⁡ 2 x d x = 1 2 ∫ cos ⁡ 3 x - 2 x - cos ⁡ ( 3 x + 2 x ) d x

= 1 2 ∫ cos ⁡ x d x - 1 2 ∫ cos ⁡ 5 x d x

Passo 3

Agora vamos resolver nossas integrais

∫ cos ⁡ x d x = sen ⁡ x

E, para resolver a integral

∫ cos ⁡ 5 x d x

Vamos utilizar a substituição

u = 5 x

d u = 5 d x

Então ficamos com

∫ cos ⁡ 5 x d x = 1 5 ∫ cos ⁡ u d u = 1 5 sen ⁡ u

∫ cos ⁡ 5 x d x = 1 5 sen ⁡ 5 x

Passo 4

Por fim, juntamos a solução das integrais do passo anterior.

∫ sen ⁡ 3 x sen ⁡ 2 x d x = 1 2 ∫ cos ⁡ x d x - 1 2 ∫ cos ⁡ 5 x d x

∫ sen ⁡ 3 x sen ⁡ 2 x d x = 1 2 sen ⁡ x - 1 2 1 5 sen ⁡ 5 x

∫ sen ⁡ 3 x sen ⁡ 2 x d x = 1 2 sen ⁡ x - 1 10 sen ⁡ 5 x + C

Resolvido! Não esquece a constante de integração viu?

Resposta

Exercícios de Livros Relacionados

Deduza uma fórmula similar àquela do Exercício 41 para ∫ cot n ⁡ x d x ,s en for um inteiro positivo maior do que 1.
Calcule a integral. ∫ 0 π 4 sec ⁡ θ tan ⁡ θ d θ
Calcular a área da região limitada por y = tg^3 x , y = 1 e x = 0 .
Calcule a integral.int s e n^2 (pi x) cos^5 ( pi x ) d x
Calcule a integral.int s e n^6 (pi x) d x