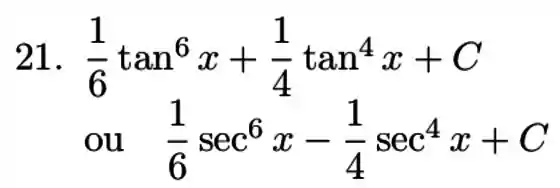Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Trigonométricas

Ver Teoria
Exercício 601234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Precisamos resolver

∫ tan 3 ⁡ x sec 4 ⁡ x d x

Vamos começar usando a identidade trigonométrica

sec 2 ⁡ x = tan 2 ⁡ x + 1

E ficamos com

∫ tan 3 ⁡ x sec 2 ⁡ x tan 2 ⁡ x + 1 d x

Passo 2

Para resolver essa integral vamos usar a substituição

u = tan ⁡ x

d u = sec 2 ⁡ x d x  

Aplicando na nossa integral vamos ficar com

∫ tan 3 ⁡ x sec 2 ⁡ x tan 2 ⁡ x + 1 d x = ∫ u 3 u 2 + 1 d u

Que podemos separar em duas integrais

∫ u 3 u 2 + 1 d u = ∫ u 5 d u + ∫ u 3 d u

Resolvendo nossas integrais ficamos com

∫ u 3 u 2 + 1 d u = u 6 6 + u 4 4 + C

Desfazendo a substituição

u = tan ⁡ x

∫ tan 3 ⁡ x sec 4 ⁡ x d x = tan 6 ⁡ x 6 + tan 4 ⁡ x 4 + C

Resolvida nossa integral!

Outra opção seria ter substituído tan 2 ⁡ x = 1 - sec 2 ⁡ x

E resolvido de forma parecida, utilizando a substituição u = sec ⁡ x . Teríamos encontrado

∫ tan 3 ⁡ x sec 4 ⁡ x d x = sec 6 ⁡ x 6 - sec 4 ⁡ x 4 + C

Resposta

Exercícios de Livros Relacionados

Deduza uma fórmula similar àquela do Exercício 41 para ∫ cot n ⁡ x d x ,s en for um inteiro positivo maior do que 1.
Calcule a integral. ∫ 0 π 4 sec ⁡ θ tan ⁡ θ d θ
Calcular a área da região limitada por y = tg^3 x , y = 1 e x = 0 .
Calcule a integral.int s e n^2 (pi x) cos^5 ( pi x ) d x
Calcule a integral.int s e n^6 (pi x) d x