UFSC – Cálculo 1 – Lista 4.8 – Questão 1d
Calcule as integrais abaixo.
Passo 1
E aí pessoal, tudo bem?
Essa questão integral complicada, mas vou ajudar você aqui! O problema nos deu essa integral trigonométrica para resolver:
E quando você vir um integrando que não tem função-derivada da função dentro dele (que é nosso caso) você testa o método de integração por partes! Como vimos lá na lista de integração por partes, você está autorizado a usar truques sujos! Isso mesmo: truquinhos que vão te ajudar a separar esse integrando em uma parte para integrar e outra para derivar, sempre usando nosso LIATE:
Lembrando que no método por partes precisamos integrar uma parte do integrando, e sabemos a integral de !
Usando o método de integração por partes, com
Poderemos integrar essa coisa!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Relembrar é viver, então vamos ao método de por partes:
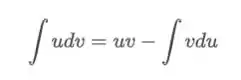
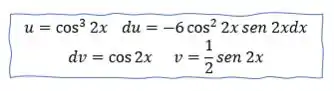
Agora vamos aplicar na fórmula do método por partes:
Vamos guardar esse resultado!
Tudo bem até aqui? Nossa missão agora é calcular aquela integral que surgiu na direita! Vamos lá?
Passo 3
A integral que surgiu na direita é:
Agora anota aí um ponto bem importante em trigonométricas, primeiro algumas identidades:
E já vamos usar a primeira!
E substituir na integração:
Vamos devolver esse resultado no passo 2?
Passo 4
Resgatando o resultado do passo 2:
E substituindo a integral do lado direito:
Parece que ficou maior, mas te garanto que ficou melhor! Vamos retirar as integrais dos colchetes:
Olha só o que temos! Achamos a mesma integral que estamos calculando do lado esquerdo! Então podemos juntar elas:
E isolar:
Calma, estamos quase lá!
Guarda mais esse resultado? Obri! =)
Passo 5
Nossa missão agora é resolver essa última integral da direita! E aqui vou colar mais um quadrinho com identidades trigonométricas bem importantes:
Precisamos resolver essa integral aqui:
Então vamos usar a terceira identidade, aí nosso integrando fica mais simples e podemos usar substituição simples para resolver, saca só:
Agora #partiu integrar?
Beleza? Vamos juntar os resultados?
Passo 6
Juntando os resultados do passo 4 com 5 temos:
Também:
Aí:
Beleza? Mas ainda não acabamos! Essa integral é DEFINIDA, então precisamos aplicar esses resultados nos limites de integração!
Passo 7
Nossos limites eram:
Agora é só aplicar!
Agora sim terminamos! E é isso!
Espero ter ajudado! Vamos para a próxima?