UNICAMP – Cálculo 1 – Lista 3 – Limite e Continuidade
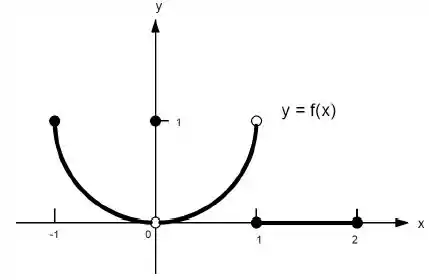
22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
e) existe
Passo 1
Falaaa... beleza??
Nessa questão vamos analisar a afirmação “ existe” e responder se ela é verdadeira ou falsa, com base no gráfico.
Pra isso vamos lembrar que quando temos um limite escrito da forma queremos saber o limite da função para valores que se aproximam de pela esquerda. De forma análoga, representa o limite para valores que se aproximam de pela direita.
Também vamos lembrar que para um limite existe, os limites laterais devem ser iguais.
Passo 2
A afirmação diz que o limite de quando está se aproximando de existe. Pro limite existe, os limites laterais devem ser iguais, então se , o limite existe.
Repara no gráfico:
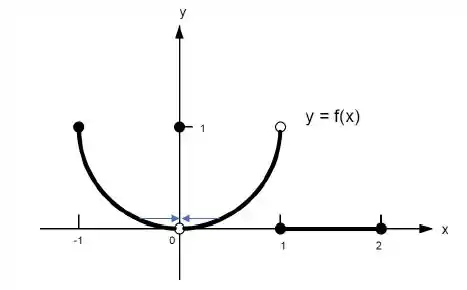
Sim, quando está se aproximando de pela direita, o limite vale e quando está se aproximando de pela esquerda, o limite também vale . Portanto, o limite existe.
ATENÇÃO para não confundir com continuidade da função, heim!? Pro limite existe, SÓ precisamos que os limites laterais sejam iguais. Já pra função ser contínua, precisamos que os limites laterais sejam iguais e que a função seja igual ao limite naquele ponto.
Verdadeira
Resposta
Verdadeira