UNICAMP – Cálculo 1 – Provas Antigas – P1 – 2022.1 - 6ª Diurno – Questão 2b
Avalie os limites abaixo e encontre o correspondente valor caso exista (sem usar a regra de L’Hospital). Justifique suas respostas.
(b)
Passo 1
Falaeee, belezinha?? Eita que essa aí dá um nozinho na cabeça né?!
Mas calmae que vai dar certinho, bora lá!!
Primeiramente temos que ter ideia que, independentemente do valor de , o valor seno é um número entre e (como mostra a figura abaixo), certo?
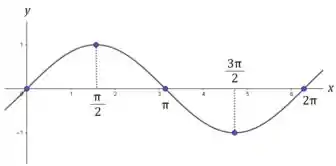
Em termos matemáticos, temos que
Observação: Note que nesse caso .
Passo 2
Dessa forma, é só pegar esse intervalo do seno que acabamos de ver adequar com a função que recebemos, se liga:
Agora vamos aplicar o limite!!
Passo 3
Assim, podemos aplicar o Teorema do Confronto, que diz que:
“Se uma função que está no meio de outras duas funções que tem o mesmo limite, então obrigatoriamente a função que está no meio terá o mesmo limite das outras duas”
Assim, vamos ver os limites dessas duas funções, ou seja:
E
Dessa forma, podemos concluir que
Entendeu direitinho? Responde aee ;)
