UFU, Sem Campus, Cálculo 1 - Listas de Cálculo 1, Questão 6.2b
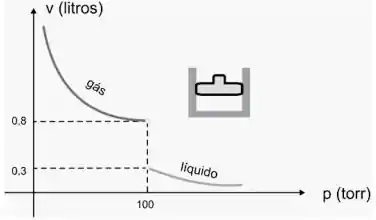
Um gás (tal como vapor d’água ou oxigênio) é mantido à temperatura constante no pistão. A medida que o gás é comprimido, o volume (V ) decresce até que atinja uma certa pressão (p) crítica. Além dessa pressão, o gás assume forma líquida. Use o gráfico da figura a seguir para resolver e interpretar.
(b)
Passo 1
Eaew, tudo certinho contigo?
Temos que encontrar o limite lateral
Então vamos lá. Vem comigo!
Passo 2
Olhando para o gráfico apresentado no enunciado, quando a pressão se aproxima de 100torr pela direita, temos que
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Exercícios de Livros Relacionados
Faça o gráfico da função f x = sin π x do Exemplo 4 na janela retangular - 1,1 por - 1,1 . Então dê um zoom em direção à origem diversas vezes. Comente o comportamento dessa função.
Estime o valor do limite lim x → 0 1 + x 1 x Com 5 casas decimais. Esse número lhe parece familiar?Confirme sua resposta da letra (a) fazendo o gráfico da função.
Esboce o gráfico de um exemplo de uma função f que satisfaça a todas as condições dadas.14)lim x → 0 - f x = 1 , lim x → 0 + f x = - 1 ,lim x → 2 - f x = 0 ,lim x → 2 + f x = 1 , f 2 = 1 ,f 0
Use o gráfico da função f x = 1 1 + e 1 x Para dizer o valor de cada limite, se existir. Se não existir, explique por quê. lim x → 0 - f x lim x → 0 + f x lim x → 0 f ( x )
Para a função f cujo gráfico é dado, diga o valor de cada quantidade indicada, se ela existir. Se não existir, diga o por quê. lim x → 1 - f x lim x → 1 + f x lim x → 1 f x lim x → 5 f x f ( 5