UFCG – Cálculo Diferencial e Integral I – AV1 – 2022.2 – Questão 5d
Calcule os limites, caso existam:
d)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para determinarmos o seguinte limite, caso exista:
E aí? Como podemos resolver? Não podemos simplesmente substituir o limite pois haverá uma indeterminação (divisão por zero).
Uma ideia é fazer uma divisão entre os polinômios do numerador e do denominador para prosseguirmos com o limite.
Não entendeu? Então bora junto 😉
Passo 2
Bom... dividindo os polinômios, temos:
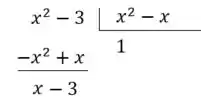
Logo, temos que:
Agora vamos aplicar no limite!!
Passo 3
Agora, aplicando no limite, temos:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Faça o gráfico da função f x = sin π x do Exemplo 4 na janela retangular - 1,1 por - 1,1 . Então dê um zoom em direção à origem diversas vezes. Comente o comportamento dessa função.
Estime o valor do limite lim x → 0 1 + x 1 x Com 5 casas decimais. Esse número lhe parece familiar?Confirme sua resposta da letra (a) fazendo o gráfico da função.
Esboce o gráfico de um exemplo de uma função f que satisfaça a todas as condições dadas.14)lim x → 0 - f x = 1 , lim x → 0 + f x = - 1 ,lim x → 2 - f x = 0 ,lim x → 2 + f x = 1 , f 2 = 1 ,f 0
Use o gráfico da função f x = 1 1 + e 1 x Para dizer o valor de cada limite, se existir. Se não existir, explique por quê. lim x → 0 - f x lim x → 0 + f x lim x → 0 f ( x )
Para a função f cujo gráfico é dado, diga o valor de cada quantidade indicada, se ela existir. Se não existir, diga o por quê. lim x → 1 - f x lim x → 1 + f x lim x → 1 f x lim x → 5 f x f ( 5