Certas fórmulas que representam quantidades físicas podem conduzir a limites que envolvam infinito. Claramente, uma grandeza física não pode tender para infinito, mas uma análise de uma situação hipotética em que tal fato pudesse ocorrer, pode sugerir usos para outras quantidades relacionadas. Vejamos os seguintes exemplos.
A lei de Ohm na teoria da eletricidade afirma que , onde é a resistência (em ohms) de um condutor, é a diferença de potencial (em volts) através do condutor e é a corrente (em ampères) que passa pelo condutor. A resistência de certas ligas tende para zero quando a temperatura se aproxima do zero absoluto (aproximadamente ), e a liga se torna um supercondutor de eletricidade. Se a voltagem é fixa, então, para esse
supercondutor,
isto é, a corrente aumenta sem limite. Os supercondutores permitem que grandes correntes sejam usadas em usinas geradoras ou motores. Eles têm também aplicações no transporte terrestre a alta velocidade, no qual o forte campo magnético produzido por magnetos supercondutores permitem que os trens levitem, não havendo essencialmente fricção entre as rodas e os trilhos. Possivelmente a utilização mais importante para os supercondutores está nos circuitos para computadores, porque esses circuitos produzem pouquíssimo calor.
Passo 1
Oi pessoal, tudo bem por aí? Essa questão nos fala sobre a Primeira Lei de Ohm que nos diz que
Quando temos uma resistência dita ôhmica, o valor da diferença de potencial pela corrente que circula em um circuito é constante
 mas e quando a voltagem é fixa?
mas e quando a voltagem é fixa?
Quando temos um circuito no qual a voltagem é fixa temos que a corrente pode ser medida através de sua resistência
E para certas ligas metálicas, quando as temperaturas estão baixas, chamamos elas de supercondutores, pois verificamos que a resistência vai à zero. E o que acontece com a corrente?
Vai à infinito! Isso porque temos um número fixo sendo dividido por um valor cada vez menor

Passo 2
Vemos aqui um gráfico que mostra a resistividade elétrica contra a temperatura para um metal comum (azul) e um supercondutor (vermelho)
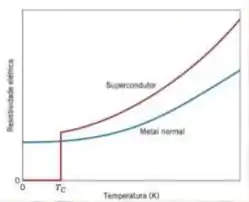
Abaixo de uma certa temperatura crítica a resistividades dos supercondutores fica tão baixa que caracterizamos como nula. E essa característica é que dá o nome a eles de supercondutores
E é isso! Até a próxima!