- Considere a fun ̧c ̃ao f cujo gr ́afico est ́a representado abaixo. Determine o que se pede.
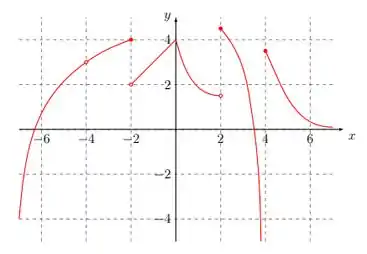
- Os limites e
- Os limites e
- Os limites e
- Os limites e
- Os limites e
- O que se pode dizer sobre a existência dos limites laterais nos pontos e ?
Passo 1
Oi, galerinha! Tudo bom? Nesta questão temos que avaliar os limites laterais de , tanto pela direita, como pela esquerda.
A questão não disse quem é , mas mostrou como é o gráfico. Então para dizer que são esses limites, vamos imaginar que estamos andando sobre a função até o ponto que está tendendo e vemos qual é o limite.
Bora lá!
Passo 2
- Vamos começar por
- Para , teremos:
- Para , teremos:
- Para , teremos:
- Para , teremos:
- Agora temos que avaliar a existência dos limites laterais nos pontos e . Note que em que todos esses pontos a função é continua, ou seja, estamos bem em cima da linha. Logo, os limites laterais serão iguais.
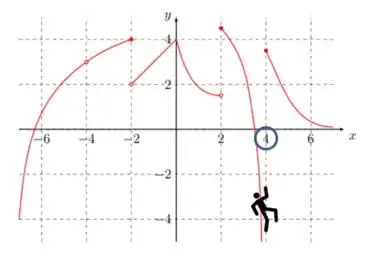
Repara que o bonequinho está escorregando para menos infinito, quando esta se aproximando do número no eixo . Logo:
Agora vamos para
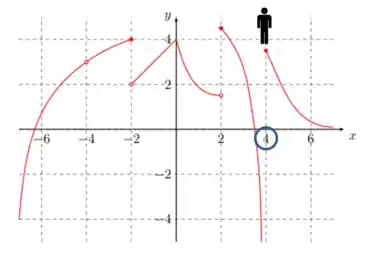
Repara que o bonequinho subiu aquela ladeira – opsss, função! – indo em direção a e chegou num ponto onde . Então:
Entendeu a ideia? Agora vamos aplicar para as outras letras!
Passo 3
Passo 4
Passo 5
Passo 6
Passo 7
Resposta
No texto.