UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Prof° Ricardo Martins - Listas sobre Limites e Continuidade, Questão 1.3
Considere a função
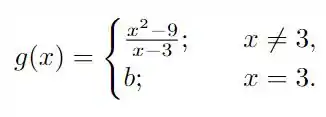
esta função tem limite em ? Qual deve ser o valor de para que a função seja contínua?
Passo 1
Eaew, belezinha?
O enunciado nos dá a seguinte função
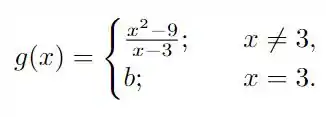
Para garantir que o limite existe, devemos verificar se
e, se quisermos garantir a continuidade, precisamos que
e, também, é preciso que
Vamos tentar fazer isso! Bora lá!
Passo 2
A primeira coisa que podemos fazer é fazer a substituição
note que isso é uma indeterminação. Portanto, temos que reescrever a função. O nosso numerador é da seguinte forma
pode ser escrito como o produto
De forma que o limite é da forma
que substituindo , é dado por
Mas, e agora como garantimos que a função é contínua? Vem comigo!
Passo 3
Os limite laterais
são iguais, uma vez que o cálculo é indiferente se analisarmos pela esquerda ou direita de . Agora, como temos que
a segunda condição requer que
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
e