Lista 3 – 2018.1 – UFES – Cálculo I – Questão 2ii
Dadas as funções:
E
(ii) Calcule e
Passo 1
Eaeee, meu consagradx!! Beleza?? Seguinte, vamos relembrar dos gráficos que vimos no exemplo anterior:
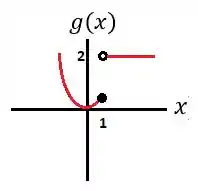
Passo 2
Agora, vamos fazer descobrir os limites das duas funções através dos limites laterais. Para isso, os limites laterais devem ter um mesmo valor, ou seja:
Passo 3
Para , percebemos pelo gráfico que:
Dessa forma, concluímos que o limite que queremos não existe pois os valores deram diferentes, ou seja:
Passo 4
Para , percebemos pelo gráfico que:
Dessa forma, concluímos que o limite que queremos não existe pois os valores deram diferentes, ou seja:
Entendeu direitinho?? Responde aí ;)
Resposta
Exercícios de Livros Relacionados
Faça o gráfico da função f x = sin π x do Exemplo 4 na janela retangular - 1,1 por - 1,1 . Então dê um zoom em direção à origem diversas vezes. Comente o comportamento dessa função.
Estime o valor do limite lim x → 0 1 + x 1 x Com 5 casas decimais. Esse número lhe parece familiar?Confirme sua resposta da letra (a) fazendo o gráfico da função.
Esboce o gráfico de um exemplo de uma função f que satisfaça a todas as condições dadas.14)lim x → 0 - f x = 1 , lim x → 0 + f x = - 1 ,lim x → 2 - f x = 0 ,lim x → 2 + f x = 1 , f 2 = 1 ,f 0
Use o gráfico da função f x = 1 1 + e 1 x Para dizer o valor de cada limite, se existir. Se não existir, explique por quê. lim x → 0 - f x lim x → 0 + f x lim x → 0 f ( x )
Para a função f cujo gráfico é dado, diga o valor de cada quantidade indicada, se ela existir. Se não existir, diga o por quê. lim x → 1 - f x lim x → 1 + f x lim x → 1 f x lim x → 5 f x f ( 5