Lista 3 – 2018.1 – UFES – Cálculo I – Questão 2i
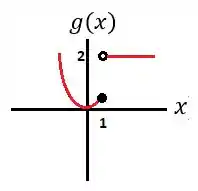
Dadas as funções:
E
- Esboce o gráfico de e
Passo 1
Fala aí!! Belezinha? Seguinte, vamos devagarinho aqui para a gente poder entender pouco a pouco.
Primeiramente, vamos esboçar o gráfico da de :
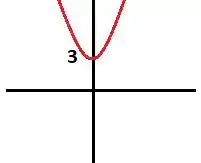
Para :
Passo 2
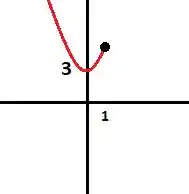
Agora, vamos esboçar o gráfico da de :
Para :
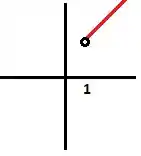
Passo 3
Assim, juntando os dois gráficos, temos que a função é dada por:
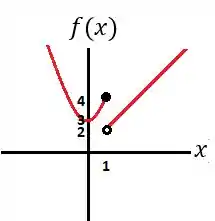
Passo 4
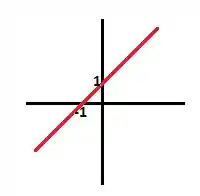
Agora, vamos esboçar o gráfico da de :
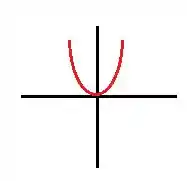
Para :
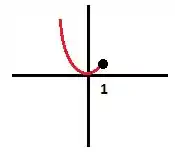
Passo 5
Agora, vamos esboçar o gráfico da de :
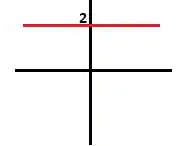
Para :
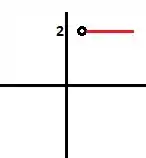
Passo 6
Assim, juntando os dois gráficos, temos que a função é dada por:
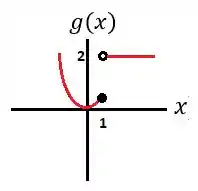
Resposta
Exercícios de Livros Relacionados
Faça o gráfico da função f x = sin π x do Exemplo 4 na janela retangular - 1,1 por - 1,1 . Então dê um zoom em direção à origem diversas vezes. Comente o comportamento dessa função.
Estime o valor do limite lim x → 0 1 + x 1 x Com 5 casas decimais. Esse número lhe parece familiar?Confirme sua resposta da letra (a) fazendo o gráfico da função.
Esboce o gráfico de um exemplo de uma função f que satisfaça a todas as condições dadas.14)lim x → 0 - f x = 1 , lim x → 0 + f x = - 1 ,lim x → 2 - f x = 0 ,lim x → 2 + f x = 1 , f 2 = 1 ,f 0
Use o gráfico da função f x = 1 1 + e 1 x Para dizer o valor de cada limite, se existir. Se não existir, explique por quê. lim x → 0 - f x lim x → 0 + f x lim x → 0 f ( x )
Para a função f cujo gráfico é dado, diga o valor de cada quantidade indicada, se ela existir. Se não existir, diga o por quê. lim x → 1 - f x lim x → 1 + f x lim x → 1 f x lim x → 5 f x f ( 5