Lista 3 – 2018.1 – UFES – Cálculo I – Questão 2iii
Dadas as funções:
E
(iii) Dê a expressão da função e verifique se existe .
Passo 1
Falaeee, beleza? Seguinte, vamos multiplicar as duas funções em seus respectivos intervalos como a questão pede e dar uma analisada:
Passo 2
Vamos também dar uma relembrada nos gráficos que descobrimos de e :
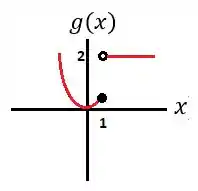
Passo 3
Podemos generalizar a expressão de para seus limites laterais, ou seja:
Substituindo pelos valores que encontramos anteriormente, temos:
Agora, para os limites laterais da direita:
Substituindo os valores que encontramos anteriormente:
Como os limites laterais deram iguais, isso quer dizer que existe e tem seu valor igual a 4, ou seja:
Legal né?? Vamos para a próxima, valeeeu!!
Resposta
Exercícios de Livros Relacionados
Faça o gráfico da função f x = sin π x do Exemplo 4 na janela retangular - 1,1 por - 1,1 . Então dê um zoom em direção à origem diversas vezes. Comente o comportamento dessa função.
Estime o valor do limite lim x → 0 1 + x 1 x Com 5 casas decimais. Esse número lhe parece familiar?Confirme sua resposta da letra (a) fazendo o gráfico da função.
Esboce o gráfico de um exemplo de uma função f que satisfaça a todas as condições dadas.14)lim x → 0 - f x = 1 , lim x → 0 + f x = - 1 ,lim x → 2 - f x = 0 ,lim x → 2 + f x = 1 , f 2 = 1 ,f 0
Use o gráfico da função f x = 1 1 + e 1 x Para dizer o valor de cada limite, se existir. Se não existir, explique por quê. lim x → 0 - f x lim x → 0 + f x lim x → 0 f ( x )
Para a função f cujo gráfico é dado, diga o valor de cada quantidade indicada, se ela existir. Se não existir, diga o por quê. lim x → 1 - f x lim x → 1 + f x lim x → 1 f x lim x → 5 f x f ( 5