UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 1ª Lista de Exercícios, Questão 10.4c.
4. Determine os seguintes limites
(c) ;
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema, nosso objetivo é obter os limites laterais da função para tendendo a 0 pela direita.
Tem ideia de como fazer isso? 🤔
O limite de uma função é um conceito fundamental da matemática que descreve o comportamento da função à medida que a variável independente se aproxima de um determinado valor.
O limite lateral de uma função é um conceito que descreve o comportamento da função à medida que a variável independente se aproxima de um determinado valor por um dos lados (esquerdo ou direito). Formalmente, o limite lateral à esquerda da função quando se aproxima de é denotado por:
Isso significa que, à medida que se aproxima de pela esquerda (ou seja, valores menores que a), a função se aproxima de um valor . O limite lateral à direita da função quando se aproxima de é denotado por:
Isso significa que, à medida que se aproxima de pela direita (ou seja, valores maiores que a), a função se aproxima de um valor .
Se ambos os limites laterais existirem e forem iguais, o limite geral da função em existe. Se os limites laterais existirem, mas não forem iguais, o limite geral da função em não existe.
Sacou? Bora começar! 😉
Passo 2
Calculando o limite quando tende a pela direita, temos
Nesse caso, podemos fazer o produto de dois limites
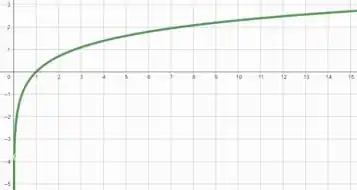
Portanto, o limite de para tendendo a pela direita é igual a pois sabemos que o gráfico de é aproximadamente igual a
Tranquilo até aqui? 🤔
Passo 3
Agora vamos calcular o limite de
Quando tende a pela direita, estamos dividindo um número relativamente alto por um número muito menor que . Ou seja quanto mais próximo de maior é o resultado dessa divisão até que cheguemos em um valor muito alto, próximo de
Juntando os dois resultados, temos
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
