UFSC; Cálculo 1; Lista 1.4 – Limites laterais; Exercício C3
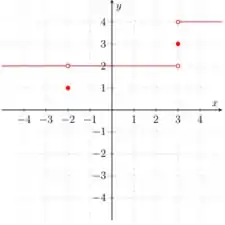
C3. Esboce o gráfico de uma função que satisfaça todas as seguintes condições: , , e .
Passo 1
Faaaala, galerinha! Tudo certinho com vocês?? Bora lá resolver mais uma questão!!
Esse é um desses exercícios bem típicos de cálculo 1, em que nos é pedido para esboçar um gráfico de uma função!
Porém, aqui o enunciado nos deu alguns limites de uma mesma função, alguns valores de pontos específicos dessa função, mas não nos deu a função em si!
Ixi, mas isso será um problema?
Relaxa! Como se trata de limites e pontos específicos, não precisamos da função para esboçar o gráfico.
Mas já adianto: por conta disso, há infinitas maneiras de se montar o gráfico.
Então, se o seu der diferente do que faremos aqui, pode ser que ele ainda esteja certo!
Bora lá então!
Passo 2
Antes de tudo vamos definir os intervalos dos pontos e limites que nos foram dados no enunciado.
O enunciado nos deu que:, , e .
Então:
- Em temos que se aproxima de 3 pela direita, então em valores maiores que 3, portanto: , ;
- Em , temos que se aproxima de 3 pela esquerda, então em valores menores que 3, portanto: , ;
- Em , temos que: , ;
- Em temos que: , ;
- Em , temos que: , .
Agora que fizemos essa avaliação, podemos relacionar os valores de e mencionados acima e montar o seguinte gráfico como exemplo:
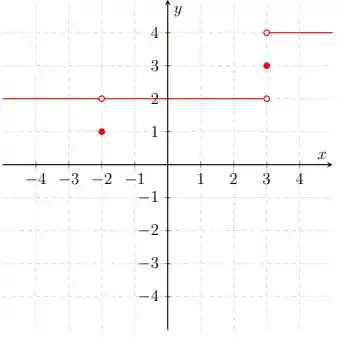
Prontinho, pessoal! Bem simples, não é mesmo?
Bora lá resolver mais uma?
Resposta
Há infinitas possibilidades de respostas. Uma delas é:
