USP, Sem Campus, Cálculo 1, Listas de C1 - Profº Fernando Manfio - Lista 4, Questão 7
Dê exemplo de uma função tal que existe, mas não existe.
Passo 1
Eaew, belezinha?
Bem… a questão é bastante direta, ela quer um exemplo de função em que
existe
e que
não existe
Aqui, a melhor forma é avaliar funções definidas por partes, e além disso, verificar que para que um limite exista, precisamos que
em que indica o limite tomado pela direita ou esquerda! Vamos fazer isso!
Passo 2
Na minha opinião, o exemplo mais simples que podemos usar é a função degrau da forma
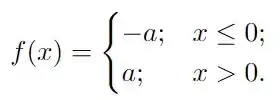
vamos tentar analisar a existência do limite desta função e de seu módulo! Note que
e
portanto, temos que
e, portanto, o limite não existe! Mas, o que acontece quando avaliamos o módulo? Saca só!
Passo 3
Quando calculamos o limite do módulo da função, temos que
quase a mesma coisa, para o outro lado no entanto, temos que
Note que agora
e, portanto, o limite existe! Sendo um exemplo do que o enunciado pediu! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos!