Lista 3 – 2018.1 – UFES – Cálculo I – Questão 3
Dê um exemplo no qual existe, mas não existe.
Passo 1
Eeeeeita!!! Calma, calma. Vamos juntos aqui que vai dar certo!!
Nessa questão, a gente precisar dar um exemplo de uma função que o limite dela não exista quando . Beleza, tem várias ne!
Mas calma, queremos que pro módulo da função, o limite exista nesse mesmo ponto... Como pode o limite da função não existir, mas o limite do módulo existir??
Vamos relembrar que pra um limite existir, precisamos que os limites laterais existam e sejam iguais. Em outras palavras, o limite tendendo pela esquerda deve ser igual ao limite tendendo pela direita.
Em que função, os limites laterais são diferentes, mas no seu módulo os limites são iguais?
Passo 2
Vamos considerar a função a seguir junto com seu gráfico:
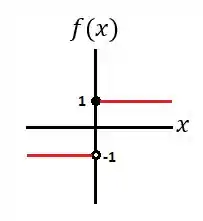
Como se observa pelo gráfico, e .
Consequentemente, como os limites laterais são diferentes entre si, confirma-se que o limite de quando tende a não existe, ou seja:
Passo 3
No entaaaanto, caso colocássemos o módulo na função , teríamos o seguinte:
Ou seja, seria uma função constante para qualquer valor de !!!!! Interessante, né?!
E, seguindo essa linha de raciocínio, quando aplicássemos os limites laterais, teríamos que:
Assim, como os limites laterais existem e são iguais, isso quer dizer que existe e é igual a 1.
Legal né?? Vamos para a próxima, valeeeu!!
Resposta
Ei, a resposta está no passo a passo :)