UTFPR, Sem Campus, Cálculo Diferencial e Integral 1, Provas - Profª Lilian Brambila - P1 2023.1, Questão 2c
Para a função cujo gráfico é dado, diga o valor de cada quantidade, se ela existir. Se não existir, explique porquê.
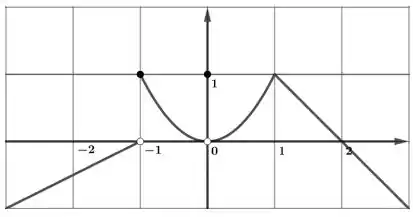
c)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para analisar o seguinte gráfico:
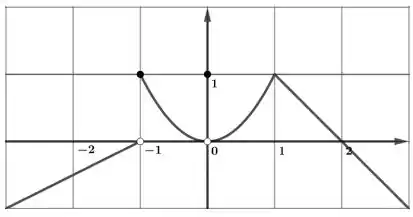
E dizer o limite de quando tende a , ou seja, quando tende a zero pela direita.
Para resolvermos isso, vamos rabiscar um pouquinho nosso gráfico, belezinha?
E aí? Bora lá??!!
😉
Passo 2
Bom... quando tende a zero pela esquerda, vemos o seguinte:
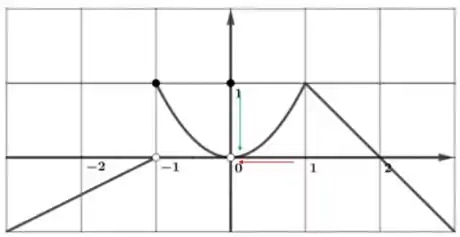
Perceba que quando (em vermelho), a linha do gráfico vai “caindo” e se aproxima de zero (em verde).
Dessa forma, podemos concluir que:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Faça o gráfico da função f x = sin π x do Exemplo 4 na janela retangular - 1,1 por - 1,1 . Então dê um zoom em direção à origem diversas vezes. Comente o comportamento dessa função.
Estime o valor do limite lim x → 0 1 + x 1 x Com 5 casas decimais. Esse número lhe parece familiar?Confirme sua resposta da letra (a) fazendo o gráfico da função.
Esboce o gráfico de um exemplo de uma função f que satisfaça a todas as condições dadas.14)lim x → 0 - f x = 1 , lim x → 0 + f x = - 1 ,lim x → 2 - f x = 0 ,lim x → 2 + f x = 1 , f 2 = 1 ,f 0
Use o gráfico da função f x = 1 1 + e 1 x Para dizer o valor de cada limite, se existir. Se não existir, explique por quê. lim x → 0 - f x lim x → 0 + f x lim x → 0 f ( x )
Para a função f cujo gráfico é dado, diga o valor de cada quantidade indicada, se ela existir. Se não existir, diga o por quê. lim x → 1 - f x lim x → 1 + f x lim x → 1 f x lim x → 5 f x f ( 5