UTFPR, Sem Campus, Cálculo Diferencial e Integral 1, Provas - Profª Lilian Brambila - P1 2023.1, Questão 2d
Para a função cujo gráfico é dado, diga o valor de cada quantidade, se ela existir. Se não existir, explique porquê.
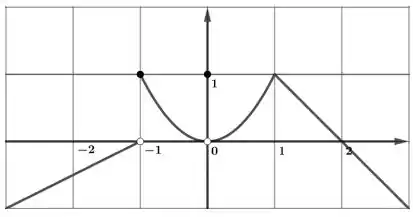
d)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para analisar o seguinte gráfico:
E nos pede para definir .
Para resolvermos isso, vamos rabiscar um pouquinho nosso gráfico e analisar os limites laterais quando tende a zero, belezinha?
E aí? Bora lá??!!
😉
Passo 2
Bom... quando tende a zero pela esquerda e pela direita, vemos o seguinte:
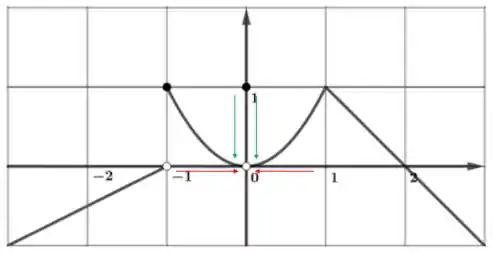
Perceba que quando pelos dois lados, vemos que .
Mas note também que há uma bolinha branca no ponto . Isso quer dizer que não está definido para .
Assim, esse valor não pertence a função.
Dessa forma, podemos afirmar o seguinte:
“ não existe pois não pode ser , porém podemos fazer analisando os limites laterais”
Entendeu direitinho? Responde aee ;)
Resposta
não existe pois não pode ser , porém podemos fazer analisando os limites laterais