C1. Para a função cujo gráfico é mostrado a seguir, determine o valor de cada quantidade, se ela existir.
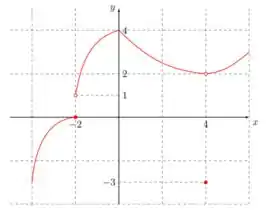
(a) . (b) . (c) . (d) .
(e) . (f) . (g) . (h) .
Passo 1
Faaaala, galerinha! Tudo certinho com vocês?? Bora lá resolver mais uma questão!!

Esse é um desses exercícios bem típicos de matemática, em que o enunciado nos pede para avaliarmos o gráfico, a partir do limite de uma função que nos foi dada.
Como temos o mesmo gráfico para todos os itens, vamos avaliar cada caso separadamente, usando de base esse gráfico!
Mas por onde começamos, para determinarmos o valor do limite a partir do gráfico?
Vamos lá resolver nos próximos passos que você já vai entender!
Bora lá então!
Passo 2
No item (a), como o enunciado pede o limite pela esquerda (isso é representado pelo sinal negativo em cima do 2 em ), vamos observar no gráfico, que quanto mais perto o eixo está de -2, mais perto de está o eixo .
Então:
Passo 3
No item (b), o enunciado pede o limite pela direita (isso é representado pelo sinal positivo em cima do 2 em ). Então vamos observar no gráfico que quanto mais perto o eixo está de , mais perto de está o eixo .
Então:
Passo 4
No item (c), como a aproximação pela esquerda é diferente da aproximação pela direita , pelo fato dessas aproximações serem diferentes, não existe limite em .
Então:
Passo 5
No item (d), o enunciado pede a imagem quando o ponto do domínio (ponto no eixo ) vale , ou seja, quando .
Então, olhando no gráfico vemos que nesse ponto, .
Passo 6
No item (e), o enunciado pede o limite pela esquerda (vindo dos números negativos), quando .
Então, observando o gráfico, quanto mais perto o eixo está de , mais perto de está o eixo .
Então:
Passo 7
Partindo para o item (f), o enunciado pede o limite pela direita (vindo dos números positivos), quando .
Observando o gráfico, quanto mais perto o eixo está de , mais perto de está o eixo .
Então:
Passo 8
No item (g), como a aproximação pela esquerda e pela direita resulta em para o eixo , temos que:
Passo 9
No item (h), observando a aproximação tanto pela direita, quanto pela esquerda, quando , ambos ficam cada vez mais perto de no eixo .
Então: .
Ufa! Terminamos!
O segredo de exercícios assim é sempre lembrar dessas propriedades chave! Então já deixa anotado no seu caderninho aí e vamo que vamo!!

Bora lá resolver mais uma questãozinha?
Resposta
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)