UFF, Niterói - Campus da Praia Vermelha, Cálculo IA, Provas de C1 - Profº Leonardo - VE1 - 2023.1, Questão 1c
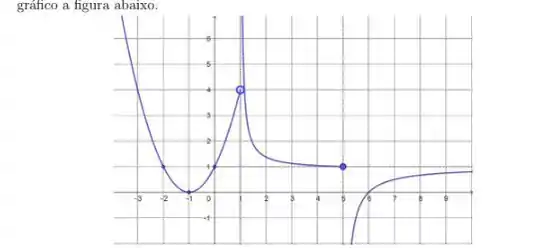
1. Uma função com domínio tem como gráfico a figura abaixo.
c.
Passo 1
Vamos calcular o limite , onde se aproxima de -1 .Primeiro, vamos considerar o termo dentro da função :
Neste termo, temos um seno no numerador e uma fração no denominador. Quando se aproxima de -1 , o denominador se aproxima de 0 , o que leva a uma indeterminação.
Passo 2
Agora, como é definida em , isso significa que a função não está definida no ponto , mas pode estar definida em . Portanto, a função pode estar definida ou não em .Nesse contexto, não podemos determinar o limite sem informações adicionais sobre como a função se comporta em torno do ponto , uma vez que a função pode ou não estar definida nesse ponto.
Resposta
Nesse contexto, não podemos determinar o limite sem informações adicionais sobre como a função se comporta em torno do ponto , uma vez que a função pode ou não estar definida nesse ponto.