UFF, Niterói - Campus da Praia Vermelha, Cálculo IA, Provas de C1 - Profº Leonardo - VE1 - 2023.1, Questão 1e A explicação está melhor, no entanto f(1) não é igual a 1. Em x=1 a função não está definida e o limite não existe.
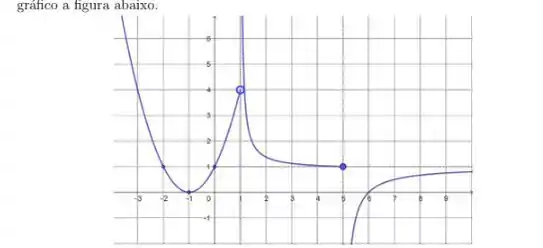
Uma função com domínio tem como gráfico a figura abaixo.
Passo 1
Para determinar o limite , onde , vamos considerar como se aproxima do infinito positivo.
A função f(x) tende a 1 quando x tende ao infinito. Isso significa que=1. No entanto, quando você compõe uma função consigo mesma, como , você está basicamente aplicando f(x) duas vezes.
Passo 2
Vamos analisar o limite de g(x) quando x tende ao infinito:
=
Agora, como =1 podemos substituir f(x) por 1:
=
Nesse ponto, você está aplicando f(x) a um valor constante (1) à medida que x tende ao infinito. Isso é equivalente a encontrar o limite de uma constante, e o limite de uma constante é simplesmente a própria constante. Portanto:
=
Passo 3
Então galera, o limite de g(x) quando x tende ao infinito é igual a 1. Não é verdade que o limite não existe. O limite de g(x) quando x tende ao infinito é bem definido e igual a 1, porque:
=1
Resposta
limx→+∞f(x)=1