UFF, Niterói - Campus da Praia Vermelha, Cálculo IA, Provas de C1 - Profº Leonardo - VE1 - 2023.1, Questão 1a
1. Uma função com domínio tem como gráfico a figura abaixo.
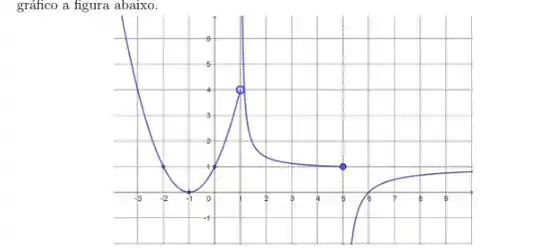
a) Estude os limites laterais e diga o que pode concluir sobre
Passo 1
Dado que a função tem o domínio , isso significa que a função está definida para todos os valores reais , exceto . Vamos estudar os limites laterais e o limite da função conforme se aproxima de 5 .
Primeiro, vamos considerar se aproximando de , ou seja, se aproximando de 5 pelo lado esquerdo:
Uma vez que está definida em , não há restrições quanto a se aproximar de 5 a partir da esquerda, pois o valor não está excluído do domínio.
Passo 2
Agora, vamos considerar se aproximando de , ou seja, se aproximando de 5 pelo lado direito:
Da mesma forma que no caso anterior, como está definida em , não há restrições quanto a se aproximar de 5 a partir da direita.
Agora, o limite refere-se ao limite no ponto . No entanto, como a função está definida em , o valor não faz parte do domínio da função. Portanto, o limite não é definido.
Resposta
e são ambos indefinidos.
é indefinido porque o valor não está no domínio da função.
Portanto, a conclusão é que a função não possui limite em , devido à exclusão do valor do domínio da função.