UFF, Niterói - Campus da Praia Vermelha, Cálculo IA, Provas de C1 - Profº Leonardo - VE1 - 2023.1, Questão 1f
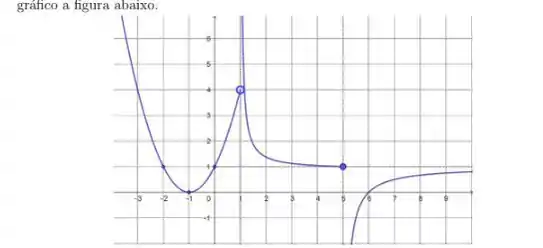
Uma função com domínio tem como gráfico a figura abaixo.
Passo 1
Vamos determinar o limite , onde , e é definida em . O valor de está se aproximando de -1 .
Primeiro, vamos analisar o comportamento de quando se aproxima de -1:
Dado que está definida para todos os valores reais exceto , podemos considerar que está definido. Portanto, está definida quando se aproxima de -1 , e é um valor real.
Passo 2
Agora, vamos considerar . Como vimos, está definida quando se aproxima de -1, e portanto também está definida.Em outras palavras, está definida quando se aproxima de -1.Portanto, o limite é simplesmente o valor da função em :
Uma vez que é um valor real (já que está definida para ), podemos calcular , que é a composição de aplicada a .
Resumindo, o limite é igual a , desde que seja um valor que não seja excluído do domínio de .
Resposta
Resumindo, o limite é igual a , desde que seja um valor que não seja excluído do domínio de .