UFF, Niterói - Campus da Praia Vermelha, Cálculo IA, Provas de C1 - Profº Leonardo - VE1 - 2023.1, Questão 1i
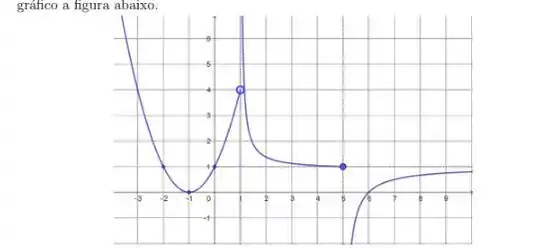
Uma função com domínio tem como gráfico a figura abaixo.
Passo 1
Para determinar o limite , onde , vamos analisar o comportamento de quando se aproxima de 5 pelo lado esquerdo.
Primeiro, vamos lembrar que o domínio de é , o que significa que está definida para todos os valores reais exceto .
Passo 2
Agora, considerando , vamos analisar como se comporta quando se aproxima de 5 pelo lado esquerdo ). Como está definida em , podemos considerar o limite .
Se o limite existe e é um valor , então quando se aproxima de 5 pelo lado esquerdo, se aproxima de . Além disso, como é definida em um intervalo em torno de , podemos considerar o limite , que nos dará o comportamento de em torno de .
Em resumo, se , então , desde que esteja definida em um intervalo em torno de .
Resposta
Portanto, o limite depende do comportamento de em torno do limite . Sem informações adicionais sobre como se comporta perto de 5 , não podemos determinar o limite de forma geral.