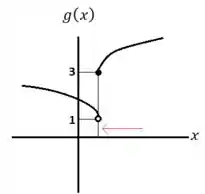
Os gráficos de e são dados. Ache os limites laterais de no ponto indicado
e
o
Ambas no ponto
Passo 1
Fala aí!! Belezinha? Seguinte, vamos devagarinho aqui para a gente poder entender pouco a pouco.
Então, nós queremos os limites laterais quando para duas funções!
Mas o que são esses limites laterais?? É quando a função tende a um valor quando aproximamos o pela esquerda e outro valor quando aproximamos pela direita.
Vou te dar um exemplo mais simples que os casos dessa questão! Olha só pra essa função descontínua:
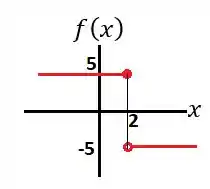
Note que quando aproximamos os valores da esquerda para direita para , ou seja, quando , então .
E, quando aproximamos os valores da direita para esquerda para , ou seja, quando , então .
Ou seja, o limite pela esquerda pode ser diferente do limite pela direita. E a gente tem que calcular ambos pras duas funções que o enunciado dá.
Mas cuidado, não são as funções que ele dá o gráfico. As nossas funções de interesse são definidas pelas duas dos gráficos
e
o
Mas vamos com calma, olhar uma de cada vez!
Passo 2
Na primeira parte da questão, a função que queremos é um produto de duas funções:
Então, primeiramente, vamos lembrar da propriedade da multiplicação dos limites:
E vamos ter que calcular isso tanto pela direita quanto pela esquerda.
Então, da propriedade, temos os seguintes limites laterais da esquerda para a direita, quando :
Pelo gráfico de percebemos que:
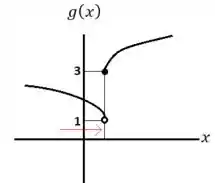
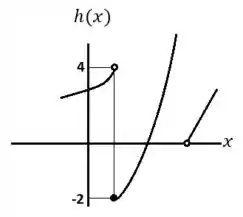
E pelo gráfico de percebemos que:
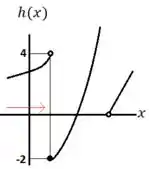
Logo, temos que:
Passo 3
Por outro lado, temos os seguintes limites laterais da direita para a esquerda, quando :
Pelo gráfico de percebemos que:
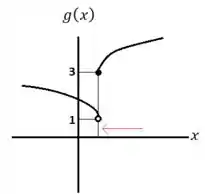
E pelo gráfico de percebemos que:
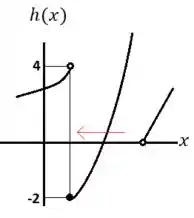
Logo, temos que:
Passo 4
Beleza! Fizemos a primeira parte... Na segunda parte temos a função composta:
o
Mas o que é essa tal de função composta???
Basicamente, ela é dada da seguinte forma:
Agora, vamos encontrar os limites laterais!!
Passo 5
Assim, temos os seguintes limites laterais da esquerda para a direita, quando :
Pelo gráfico de percebemos que:
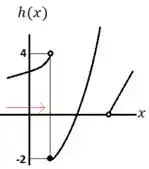
Passo 6
Assim, temos os seguintes limites laterais da direita para a esquerda, quando :
Pelo gráfico de percebemos que: