UFES, 2018.1, Lista 4, Q01
1) Os gráficos de e são dados. Ache os limites laterais de no ponto indicado.
, no ponto
Passo 1
Eaí galerinha, bora começar essa lista com o pé direito!!
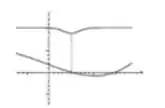
A primeira pergunta que a gente se faz é como descobrir se não tem nenhum número no gráfico né?! Mas calma, tem um número sim. O vale zero. Além disso, também podemos ver que . Outra informação importante para notarmos é que ambas as funções são contínuas, então:
Passo 2
Como no enunciado é pedido para calcularmos os limites laterais, vamos lá!!
- , pois à esquerda de ambas as funções são positivas e tende a zero.
- , pois à direita de é positiva, mas é negativa e tende a zero.
Resposta
Exercícios de Livros Relacionados
Faça o gráfico da função f x = sin π x do Exemplo 4 na janela retangular - 1,1 por - 1,1 . Então dê um zoom em direção à origem diversas vezes. Comente o comportamento dessa função.
Estime o valor do limite lim x → 0 1 + x 1 x Com 5 casas decimais. Esse número lhe parece familiar?Confirme sua resposta da letra (a) fazendo o gráfico da função.
Esboce o gráfico de um exemplo de uma função f que satisfaça a todas as condições dadas.14)lim x → 0 - f x = 1 , lim x → 0 + f x = - 1 ,lim x → 2 - f x = 0 ,lim x → 2 + f x = 1 , f 2 = 1 ,f 0
Use o gráfico da função f x = 1 1 + e 1 x Para dizer o valor de cada limite, se existir. Se não existir, explique por quê. lim x → 0 - f x lim x → 0 + f x lim x → 0 f ( x )
Para a função f cujo gráfico é dado, diga o valor de cada quantidade indicada, se ela existir. Se não existir, diga o por quê. lim x → 1 - f x lim x → 1 + f x lim x → 1 f x lim x → 5 f x f ( 5