UFF, Cálculo IA-Lista 4, GMA, 2008-1, Questão 2
Os gráficos de e são dados. Ache os limites laterais de no ponto indicado.
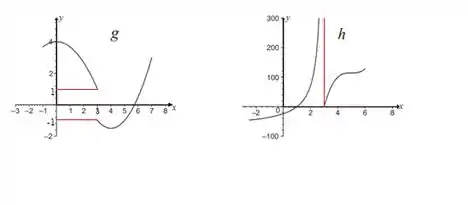
Passo 1
Não sabemos como é o gráfico de , mas com a propriedade
podemos calcular os limites laterais de no ponto .
Passo 2
Começaremos achando os limites laterais de no ponto . Olhando para o gráfico de , podemos ver que ao se aproximar de 3 pela esquerda a função se aproxima de .
Quando se aproxima de 3 pela direita, seu valor se aproxima de .
Passo 3
Agora os limites laterais de . Olhando para o gráfico dessa função vemos que:
Passo 4
Finalmente, pela propriedade enunciada no Passo 1, podemos descobrir os limites laterais de .
Resposta
Exercícios de Livros Relacionados
Faça o gráfico da função f x = sin π x do Exemplo 4 na janela retangular - 1,1 por - 1,1 . Então dê um zoom em direção à origem diversas vezes. Comente o comportamento dessa função.
Estime o valor do limite lim x → 0 1 + x 1 x Com 5 casas decimais. Esse número lhe parece familiar?Confirme sua resposta da letra (a) fazendo o gráfico da função.
Esboce o gráfico de um exemplo de uma função f que satisfaça a todas as condições dadas.14)lim x → 0 - f x = 1 , lim x → 0 + f x = - 1 ,lim x → 2 - f x = 0 ,lim x → 2 + f x = 1 , f 2 = 1 ,f 0
Use o gráfico da função f x = 1 1 + e 1 x Para dizer o valor de cada limite, se existir. Se não existir, explique por quê. lim x → 0 - f x lim x → 0 + f x lim x → 0 f ( x )
Para a função f cujo gráfico é dado, diga o valor de cada quantidade indicada, se ela existir. Se não existir, diga o por quê. lim x → 1 - f x lim x → 1 + f x lim x → 1 f x lim x → 5 f x f ( 5