Lista 3 – 2018.1 – UFES – Cálculo I – Questão 5a
Sabe-se que e é definida em ℝ. Todas as afirmativas abaixo são falsas. Tente desenhar um contra - exemplo para cada uma delas.
- para
Passo 1
Seja o gráfico de uma função arbitrária dado a seguir:
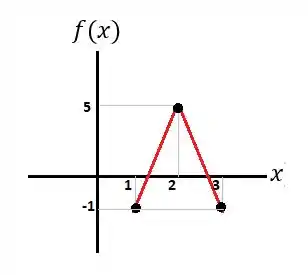
Passo 2
Nesse caso, vemos que os limites laterais existem e são iguais a , quando tende a . Ou seja:
Além disso, verificamos também que não é positiva para o intervalo entre e , portanto, a afirmação apresentada na questão está comprovada como falsa!!
Legal essa né? Vamo que vamo!!
Resposta
Afirmativa falsa
Exercícios de Livros Relacionados
Faça o gráfico da função f x = sin π x do Exemplo 4 na janela retangular - 1,1 por - 1,1 . Então dê um zoom em direção à origem diversas vezes. Comente o comportamento dessa função.
Estime o valor do limite lim x → 0 1 + x 1 x Com 5 casas decimais. Esse número lhe parece familiar?Confirme sua resposta da letra (a) fazendo o gráfico da função.
Esboce o gráfico de um exemplo de uma função f que satisfaça a todas as condições dadas.14)lim x → 0 - f x = 1 , lim x → 0 + f x = - 1 ,lim x → 2 - f x = 0 ,lim x → 2 + f x = 1 , f 2 = 1 ,f 0
Use o gráfico da função f x = 1 1 + e 1 x Para dizer o valor de cada limite, se existir. Se não existir, explique por quê. lim x → 0 - f x lim x → 0 + f x lim x → 0 f ( x )
Para a função f cujo gráfico é dado, diga o valor de cada quantidade indicada, se ela existir. Se não existir, diga o por quê. lim x → 1 - f x lim x → 1 + f x lim x → 1 f x lim x → 5 f x f ( 5