4. Seja
- Determine as quantidades a seguir, se existirem
- Esboce o gráfico de
Passo 1
- Oi, galerinha! Tudo bom? Aqui nós temos alguns limites para resolver. Vamos começar pelo primeiro.
- Aqui ele quer saber o , mas antes temo que ver se ele existe. Para isso acontecer, temos que os limites laterais devem ser iguais.
- Agora precisamos saber quanto é , ou seja, que valor a função assume quando . Olhando para a nossa , temos que
- Aqui ele quer saber o , mas antes temo que ver se ele existe. Para isso acontecer, temos que os limites laterais devem ser iguais.
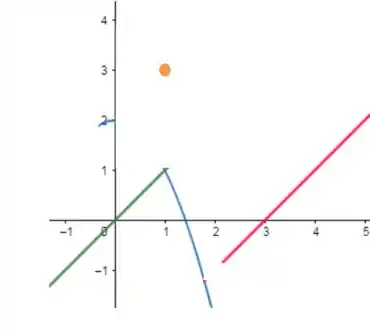
- Agora vamos esboçar esse gráfico, respeitando cada mudança de comportamento da função. Então a ideia é constuir em partes e fazer um gráfico único:
Repara que em é um ponto ondea função tem uma mudança de comportamento.
Para valores de menores que , a função tem essa cara . Logo, para calcular , vamos usar essa parte da função. Fica assim:
Prontinho! Vamos para a próxima!
Passo 2
Já calculamos quanto era . Agora vamso calcular :
Como,
Temos que
Passo 3
Passo 4
Repara que em é outro ponto onde a função tem uma mudança de comportamento.
Para valores de menores que , a função tem essa cara . Logo, para calcular , vamos usar essa parte da função. Fica assim:
Passo 5
Já vimos que em é outro ponto onde a função tem uma mudança de comportamento.
Para valores de maiores que , a função tem essa cara . Logo, para calcular , vamos usar essa parte da função. Fica assim:
Passo 6
Porém, como verificamos nos passos anteriores, esses limites são diferentes.
Logo, não existe!
Passo 7
Resposta
No texto.