3. Seja
- Encontre e .
- existe?
- existe?
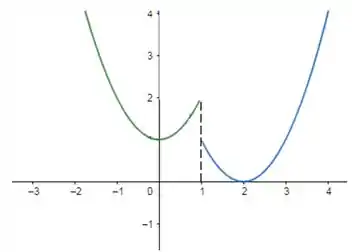
- Esboce o gráfico de
Passo 1
- Oi, galerinha! Tudo bom? Aqui nós temos dois limites para resolver. Ambos tendem a , mas um é pela esquerda e outra pela direita.
- Aqui ele quer saber se existe. Para isso acontecer, temos que os limites laterais devem ser iguais.
- Agora temos que verificar se existe. Mas nesse ponto não temos uma mudança de comportamento da função. Então podemos calcular esse limite normalmente.
- Para esboçar esse gráfico, temos que fazer primeiro a parte , para valores de . E depois fazemos a parte , para valores de . Juntando as duas partes, ele ficará assim:
Repara também que é justamente em , que a função tem uma mudança de comportamento.
Para valores de menores que , a função tem essa cara . Logo, para calcular , vamos usar essa parte da função. Fica assim:
Já para , vamos usar a parte . Fica assim:
Prontinho! Vamos para a próxima!
Passo 2
Porém, como verificamos na letra a, esses limites são diferentes.
Logo, não existe!
Passo 3
Como é menor que , vamos usar essa parte da função .
Como independente do lado que eu tiver vindo, eu chegarei em (porque essa função é contínua), então o existe!
Passo 4
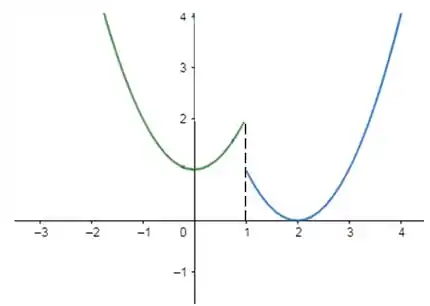
Resposta
- e
- Não existe
- Existe