Exercícios Resolvidos de Limites Laterais e Existência do Limite

Exercício 166 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100

Enunciado

Lista 3 – 2018.1 – UFES – Cálculo I – Questão 4a

Se para todo e , verifique se as afirmativas abaixo são verdadeiras ou falsas. Caso seja verdadeira, apresente uma justificativa. Caso seja falsa, apresente um contra-exemplo.

não existe.

Passo 1

Oooopa!! Já vou te falando que essa afirmativa aí é FALSA porque os limites laterais podem tender a , fazendo com que o limite dessa função também seja !!

(Só lembrando que se um limite lateral for igual ao outro, quer dizer que a o limite da função existe e é igual ao resultado dos limites laterais hehe)

Agora vamos ver um contra-exemplo!!

Passo 2

Seja a seguinte função :

Para deixar mais claro, vamos fazer um esboço:

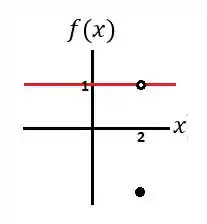
Nesse caso, os limites laterais de quando tende a existem e são iguais a 1. Ou seja, independentemente do valor de teos que:

Entendeu?? Responde aí e vamos para a próxima ;)

Resposta

Afirmativa falsa

Exercícios de Livros Relacionados

Faça o gráfico da função f x = sin ⁡ π x do Exemplo 4 na janela retangular - 1,1 por - 1,1 . Então dê um zoom em direção à origem diversas vezes. Comente o comportamento dessa função.

Estime o valor do limite lim x → 0 ⁡ 1 + x 1 x Com 5 casas decimais. Esse número lhe parece familiar?Confirme sua resposta da letra (a) fazendo o gráfico da função.

Esboce o gráfico de um exemplo de uma função f que satisfaça a todas as condições dadas.14)lim x → 0 - ⁡ f x = 1 , lim x → 0 + ⁡ f x = - 1 ,lim x → 2 - ⁡ f x = 0 ,lim x → 2 + ⁡ f x = 1 , f 2 = 1 ,f 0

Use o gráfico da função f x = 1 1 + e 1 x Para dizer o valor de cada limite, se existir. Se não existir, explique por quê. lim x → 0 - ⁡ f x lim x → 0 + ⁡ f x lim x → 0 ⁡ f ( x )

Para a função f cujo gráfico é dado, diga o valor de cada quantidade indicada, se ela existir. Se não existir, diga o por quê. lim x → 1 - ⁡ f x lim x → 1 + ⁡ f x lim x → 1 ⁡ f x lim x → 5 ⁡ f x f ( 5