Encontre, se existirem, as assíntotas horizontas e verticais do gráfico da função.
Resposta
Acho válido antes de partirmos para o vamos ver, dar uma relembrada nessas assíntotas. Sabemos que assíntotas são retas (verticais ou horizontais). Essas retas tem uma característica de a função sempre se aproximarem dela, mas nuca encostar-se a elas.
Exemplo de assíntotas:
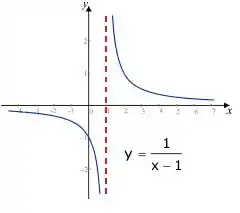
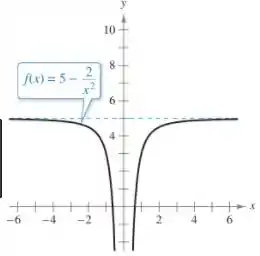
- Para averiguar calcular as possíveis assíntotas verticais, sempre buscamos um ponto onde a função pode dar problema, como no exemplo esse ponto é o :
- Para averiguar a assíntota horizontal, como no exemplo ...
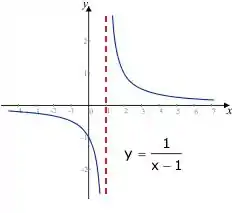
E calculemos o limite de tendendo a esse ponto. Se o limite for para o infinito, ela tem uma assíntota vertical, saca?
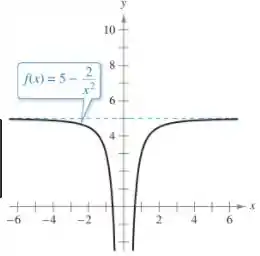
Calculemos o limite da função indo para os infinitos. Se ela der um número... Esse número será a assíntota (nesse exemplo aí, a assíntota horizontal é o
Passo 2
Então primeiro calculemos as assíntotas verticais. Sabemos que a função que queremos no nosso caso...
Como o cara de dentro do deve ser maior que ...
Então é o nosso primeiro ponto a averiguar (então averiguemos apenas o lado direito afinal ele nem está definido no esquerdo)...
Passo 3
Para resolver esse limite, apenas note que quando vai para pela direita...
Podemos derivar utilizando L’Hopital caso tenhamos uma indeterminação do tipo
Para isso, fazemos...
Aplicando L’Hopital...
Como o limite quando vai a é um número e não ao infinito, não existe assíntotas verticais.
Passo 5
Agora então, busquemos as assíntotas horizontais (se existirem). Para isso, basta a gente aplicar o limite de no infinito. Se aparecer algum número, esse número é a assíntota, saca?
Como vai ao infinito e também, o produto também vai, logo:
Deveríamos avaliar o limite no infinito negativo também, porém o não admite valores negativos. Então, como o único limite possível não deu um valor real, não existe assíntotas horizontais.
Resposta
Não existem assíntotas verticais e ou horizontais.