Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Regra de L’Hospital – Outras Indeterminações

Ver Teoria
Exercício 861234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848587888990919293949596979899100

Enunciado

UFES, Cálculo I, P2, 2020.2, questão 4a

Use a Regra de L'Hôspital e as propriedades para calcular os seguintes limites:(Justifique cada etapa do cálculo indicando as propriedades usadas).

(a) lim x → ∞ ⁡ 1 + 3 x x

Passo 1

Faaaala, galeraaaa! Tudo belezinha?

Para resolver essa questão vamos relembrar as propriedades de limites. Veja abaixo.

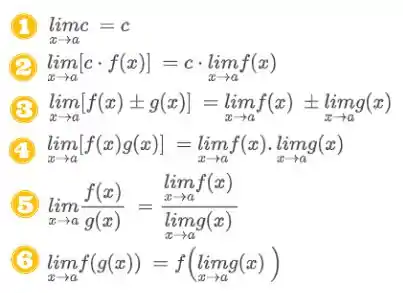
Além dessas, temos propriedades mais específicas, mostradas abaixo:

Você pode aprender mais sobre elas neste link.

Passo 2

Vamos identificar a indeterminação do limite.

lim x → ∞ ⁡ 1 + 3 x x = lim x → ∞ ⁡ 1 + 3 ∞ ∞ = ( 1 + 0 ) ∞ = 1 ∞

Então precisamos tirar a indeterminação para continuar o cálculo.

Passo 3

Vamos aplicar a função logarítmica em ambos os lados da equação. Temos que:

lim x → ∞ ⁡ y = lim x → ∞ ⁡ 1 + 3 x x

lim x → ∞ ⁡ ln ⁡ ( y ) = lim x → ∞ ⁡ xln ⁡ 1 + 3 x

Indeterminação: ∞ ∙ 0

Logo, podemos

lim x → ∞ ⁡ ln ⁡ ( y ) = lim x → ∞ ⁡ xln ⁡ 1 + 3 x = lim x → ∞ ⁡ ln ⁡ 1 + 3 x x

Indeterminação: 0 0

Só podemos aplicar L’Hospital caso a indeterminação seja 0 0 . Com esta regra, podemos facilitar nossos cálculos usando somente derivas e manipulação algébrica até obter um valor.

Aplicando L’Hospital obtemos:

lim x → ∞ ⁡ ln ⁡ ( y ) = lim x → ∞ ⁡ ln ⁡ 1 + 3 x x

Reorganizando:

lim x → ∞ ⁡ ln ⁡ ( y ) = lim x → ∞ ⁡ ln ⁡ 1 1 + 1 x + 1 x 2 - 1 x 2 = 1

lim x → ∞ ⁡ ln ⁡ ( y ) = 1

Aplicando a propriedade logarítmica novamente, obtemos:

ln ⁡ lim x → ∞ ⁡ y = 1

lim x → ∞ ⁡ y = e 1

lim x → ∞ ⁡ 1 + 3 x x = e 1

Prontinho, até mais!

Resposta

lim x → ∞ ⁡ 1 + 3 x x = e 1

Exercícios de Livros Relacionados

Use a regra de L’Hopital para determinar o seguinte exercício: l i m x → ∞ x 1 / l nx
Determine o limite:underset(x - 0^+)(lim) (1 + (1)/(x))^x
Determine o limite:underset(x - oo)(lim) ((x^2 + 1)/(x + 2))^((1)/(x))
Use a regra de L’Hopital para determinar o seguinte exercício: l i m x → 0 + x 2 l nx
Encontre o limite. Use a regra de L’Hôspital quando for apropriado. Se houver um método mais elementar, considere utilizá-lo. Se a regra de L’Hôspital não se aplicar, o porquê. l i m x → 0 x x - 1 ln