UFES, Cálculo I, P2, 2020.2, questão 4d
Use a Regra de L'Hôspital e as propriedades para calcular os seguintes limites:(Justifique cada etapa do cálculo indicando as propriedades usadas).
(d)
Passo 1
Faaaala, galeraaaa! Tudo belezinha?
Essa questão pede pra gente calcular um limite. E ela já dá a dica de que precisamos usar as propriedades e a Regra de L’Hospital ne. Então bora!
Para resolver essa questão vamos relembrar as propriedades de limites. Veja abaixo.
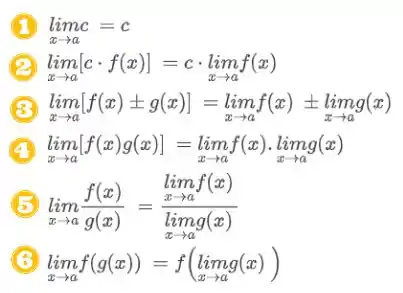
Além dessas, temos propriedades mais específicas, mostradas abaixo:
Você pode aprender mais sobre elas neste link.
Passo 2
Vamos identificar a indeterminação do limite.Agora vamos começar o cálculo substituindo o por , pra ver o que rola:
Opa! Uma indeterminação. Já era de se esperar, já que o enunciado fala em L’Hospital!
Só que a regrinha de L’Hospital não é pra qualquer tipo de indeterminação. É pra e pra
Então precisamos dar um jeito tirar essa indeterminação para continuar o cálculo.
Passo 3
Vamos reescrever a equação para obter um novo tipo de indeterminação. Temos que:
Agora podemos verificar novamente a indeterminação, temos:
Indeterminação:
Podemos agora aplicar L’Hospital. Com esta regra, podemos facilitar nossos cálculos usando somente derivadas e manipulação algébrica até obter um valor.
O que a gente fazer é substituir o numerador e o denominador da nossa função pelas suas respectivas derivadas, olha só.
Aplicando L’Hospital obtemos:
Aplicando a propriedade :
Prontinho, até mais!
