UFES, Cálculo I, P2, 2020.2, questão 4c
Use a Regra de L'Hôspital e as propriedades para calcular os seguintes limites:(Justifique cada etapa do cálculo indicando as propriedades usadas).
(b)
Passo 1
Faaaala, galeraaaa! Tudo belezinha?
Para resolver essa questão vamos relembrar as propriedades de limites. Veja abaixo.
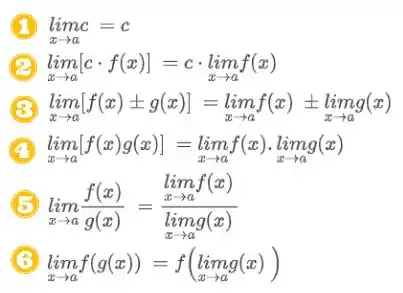
Além dessas, temos propriedades mais específicas, mostradas abaixo:
Você pode aprender mais sobre elas neste link.
Passo 2
Vamos primeiramente verificar a indeterminação deste limite.
Indeterminação:
Para aplicar L’Hospital precisamos da indeterminação . Pela propriedade 3, temos:
Peala propriedade de logaritmos, temos:
Reescrevendo:
Podemos então aplicar a propriedade 2, já que temos um produto.
Substituindo o limite
Prontinho, até mais!
Resposta
Exercícios de Livros Relacionados
Use a regra de L’Hopital para determinar o seguinte exercício: l i m x → ∞ x 1 / l nx
Determine o limite:underset(x - 0^+)(lim) (1 + (1)/(x))^x
Determine o limite:underset(x - oo)(lim) ((x^2 + 1)/(x + 2))^((1)/(x))
Use a regra de L’Hopital para determinar o seguinte exercício: l i m x → 0 + x 2 l nx
Encontre o limite. Use a regra de L’Hôspital quando for apropriado. Se houver um método mais elementar, considere utilizá-lo. Se a regra de L’Hôspital não se aplicar, o porquê. l i m x → 0 x x - 1 ln