Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 108123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

31) Calcule o trabalho realizado pelo campo de forças F → x ,   y ,   z = 2 x + z 2 i → + 2 y + x 2 j → + 2 z + y 2 k → quando uma partícula se move sob sua influência ao redor da borda da esfera x 2 + y 2 + z 2 = 4 que está no primeiro octante, no sentido anti-horário quando vista de cima.

Passo 1

Pow, trabalho de um campo de forças F → em cima de uma curva C é pra gente a essa altura do campeonato o cálculo de uma integral de linha:

∫ C   F → ⋅ d r →

Uma integral de linha como essa a gente sabe que tem dois meios basicamente que podemos resolver:

1º - Resolver pelo método diretão.

2º - Resolver pelo teorema de Stokes.

Pow, queremos uma integral de linha de um campo nada bonito sobre uma curva também não muito bonita (mesmo sem saber quem ela é a gente já pode perceber que ela não é algo trivial). Isso já é um indício de que o melhor caminho seguirmos é o teorema de Stokes.

Mas se você quer uma prova mais visual podemos calcular o Rotacional de F → ...

r o t   F → = ∂ F 3 ∂ y - ∂ F 2 ∂ z ,   ∂ F 1 ∂ z - ∂ F 3 ∂ x ,   ∂ F 2 ∂ x - ∂ F 1 ∂ y

Como

F → x ,   y ,   z = 2 x + z 2 , 2 y + x 2 ,   2 z + y 2       →

Então...

r o t   F → = 2 y - 0 ,   2 z - 0 ,   2 x - 0 →

r o t   F → = 2 y ,   2 z ,   2 x

Pow, com um rotacional desse é a prova visual de que Stokes pode ser bem mais elegante, saca?

Passo 2

“Tá bom, entendi que é pra usar Stokes, mas agora quem é mesmo esse cara? Ou melhor o que o teorema dele nos representa?”

Bem basicamente ele iguala a integral de linha com uma de superfície dessa forma aqui:

∫ C   F → ⋅ d r → = ∬ S   r o t   F → ⋅ n →   d S

Assim, ao invés de termos que calcular uma integral de linha, podemos calcular uma integral de superfície 😉!

Porém Stokes não é só isso! Se não taria muito bom, ne? Para aplicar a igualdade entre as integrais antes devemos averiguar as condições desse Teorema, que nos pede basicamente três coisas:

1º - Uma curva fechada C delimitando uma superfície S .

2º - Sem singularidades na função Vetorial.

3º - Superfície orientada positivamente.

Vamos passar por cada um deles e verificar se satisfazem ou não 😊!

Passo 3

A curva C dada no problema é a intersecção da esfera de raio 2 com os planos coordenados...

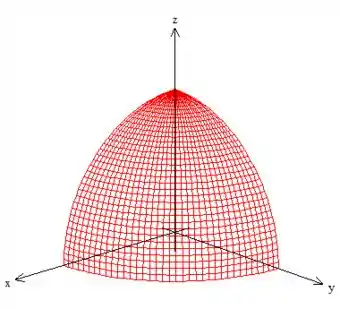
Veja a curva aí! Vou destaca-la melhor pra você:

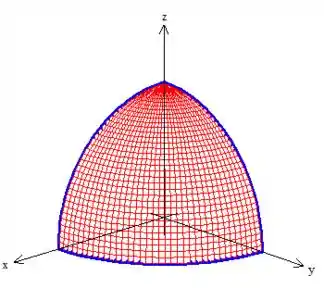
A curva é fechada sim e uma superfície que sem dúvidas é delimitada por ela é esse pedacinho de esfera no primeiro octante, saca?

A essa superfície, vamos dar o nome de Superfície S (é apenas um nome carinhoso para sabermos quem se trata 😉)

Passo 4

A outra condição é:

2º - Sem singularidades na função Vetorial.

Ora, sim! Basta ver o campo F →

F x ,   y ,   z = 2 x + z 2 , 2 y + x 2 ,   2 z + y 2

Para você perceber que o campo não tem nenhum bug ou singularidade, como uma divisão por 0 em algum ponto ou algo assim.

Passo 5

3º - Superfície orientada positivamente.

Aqui o que temos que fazer é garantir que o conjunto curva-superfície esteja orientadas positivamente, ou seja, como a curva no x y gira no senti anti-horário... Pela regra da mão direita temos que ter um vetor normal pra cima na superfície

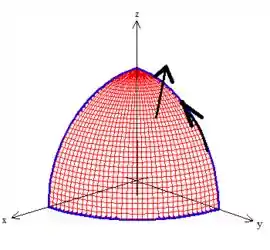
Agora elas estão sim orientadas positivamente, saca?

Passo 6

Com as condições averiguadas e sendo satisfeitas, podemos aplicar a igualdade numa nice:

∫ C   F → ⋅ d r → = ∬ S   r o t   F → ⋅ n →   d S

Para calcular a integral de superfície, precisamos:

1º - Parametrizar a superfície S .

2º - Encontrar o termo n →   d S .

Bora?

Passo 7

Para parametrizar a superfície saca só: estamos em cima de uma circunferência...

x 2 + y 2 + z 2 = 4

Podemos então parametrizar utilizando as primas das coordenadas esféricas:

x = R sin ⁡ φ cos ⁡ θ

y = R sin ⁡ φ sin ⁡ θ

z = R cos ⁡ φ

A diferença entre a parametrização de uma superfície para as coordenadas esféricas é que a a parametrização precisa apenas de 2 parâmetros (uma superfície é de 2 D ), logo aquele R ali some. Ele some virando o Raio do pedaço da esfera que é 2 ...

x = 2 sin ⁡ φ cos ⁡ θ

y = 2 sin ⁡ φ sin ⁡ θ

z = 2 cos ⁡ φ

Então a parametrização fica sendo...

σ φ ,   θ = 2 sin ⁡ φ cos ⁡ θ , 2 sin ⁡ φ sin ⁡ θ , 2 cos ⁡ φ  

Passo 8

Para os limites de φ e θ basta comparar a região que temos

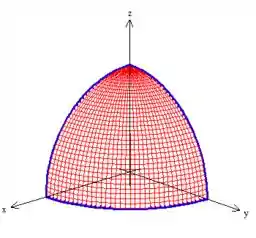
Com o gráfico de onde variam esses caras (sempre é bom saber de có essa mudança pois ela é aparece muito):

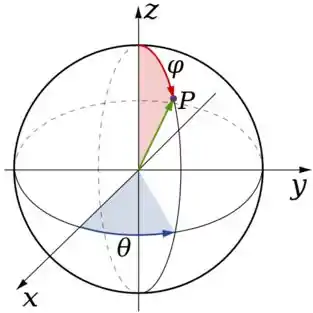
Comparando as duas a gente conclui que φ varia de 0 até 90 ° ...

0 ≤ φ ≤ π 2

E θ também...

0 ≤ θ ≤ π 2

Passo 9

Para o termo n →   d S ...

n → d S = N →   d φ d θ

Onde o N → sempre se pode obter fazendo...

N → = ∂ σ φ ,   θ ∂ φ × ∂ σ φ ,   θ ∂ θ

Mas acontece que esse produto vetorial é chato e longo. Como esferas centradas na origem aparecem tipo muito em tudo, é bom ter um macetizinho para o vetor normal dele neh? E temos sim 😊!!!

O Vetor normal de esferas na origem é:

N → = R sin ⁡ φ ⋅ σ φ ,   θ

Onde R sin ��� φ se parece com o Jacobiano láaaa nas mudanças esféricas, mas é um R só e não R 2 😉. Como o raio agora é conhecido e a σ   também...

N → = 2 sin ⁡ φ ⋅ 2 sin ⁡ φ cos ⁡ θ , 2 sin ⁡ φ sin ��� θ , 2 cos ⁡ φ     →

N → = 4 sin 2 ⁡ φ cos ⁡ θ ,   4 sin 2 ⁡ φ sin ⁡ θ , 4 sin ⁡ φ cos ⁡ φ    

Ahhhh! Veja que esse vetor normal atende lá as condições de termos o vetor normal pra cima, pois a coordenada z é positiva (o seno e o cosseno são positivos com as variações de φ e θ ). Se não atendesse era só inverter o sinal ;D

Então...

n → d S = 4 sin 2 ⁡ φ cos ⁡ θ ,   4 sin 2 ⁡ φ sin ⁡ θ , 4 sin ⁡ φ cos ⁡ φ     d φ d θ

Passo 10

Vamos antes de voltar para a integral só fazer mais uma coisinha:

Tá vendo o rotacional

r o t F → = 2 y ,   2 z ,   2 x

Perceba que ele ainda está nas coordenadas antigas. Então mudemos isso já que...

x = 2 sin ⁡ φ cos ⁡ θ

y = 2 sin ⁡ φ sin ⁡ θ

z = 2 cos ⁡ φ

r o t F → = 4 sin ⁡ φ sin ⁡ θ ,   4 cos ⁡ φ ,   4 sin ⁡ φ cos ⁡ θ

Passo 11

Jogando esses dados então na integral de superfície...

∬ S   r o t   F → ⋅ n →   d S = ∬ D   4 sin ⁡ φ sin ⁡ θ ,   4 cos ⁡ φ ,   4 sin ⁡ φ cos ⁡ θ ⋅ 4 sin 2 ⁡ φ cos ⁡ θ ,   4 sin 2 ⁡ φ sin ⁡ θ , 4 sin ⁡ φ cos ⁡ φ     d φ d θ =

Calculando esse produto interno gigante com a esperança disso simplificar ainda...

∬ D   16 sin 3 ⁡ φ sin ⁡ θ cos ⁡ θ +   16 cos ⁡ φ sin 2 ⁡ φ sin ⁡ θ + 16 cos ⁡ φ sin 2 ⁡ φ cos ⁡ θ   d φ d θ =

16 ∬ D   sin 3 ⁡ φ sin ⁡ θ cos ⁡ θ + cos ⁡ φ sin 2 ⁡ φ sin ⁡ θ + cos ⁡ θ   d φ d θ =

É, infelizmente não simplifica mais que isso, agora é só substituir os limites de φ   e θ encontrados e meter bronca! Bora?

Passo 12

16 ∫ 0 π 2 ∫ 0 π 2 sin ⁡ φ sin ⁡ φ 2 sin ⁡ θ cos ⁡ θ + cos ⁡ φ sin 2 ⁡ φ sin ⁡ θ + cos ⁡ θ d φ d θ =

Lembrando que sin 2 ⁡ φ = 1 - cos 2 ⁡ φ ...

16 ∫ 0 π 2 ∫ 0 π 2 sin ⁡ φ 1 - cos 2 ⁡ φ sin ⁡ θ cos ⁡ θ + cos ⁡ φ sin 2 ⁡ φ sin ⁡ θ + cos ⁡ θ d φ d θ =

16 ∫ 0 π 2 ∫ 0 π 2 sin ⁡ φ sin ⁡ θ cos ⁡ θ - sin ⁡ φ cos 2 ⁡ φ sin ⁡ θ cos ⁡ θ + cos ⁡ φ sin 2 ⁡ φ sin ⁡ θ + cos ⁡ θ d φ d θ

Integrando em φ ...

16 ∫ 0 π 2 - cos ��� φ sin ⁡ θ cos ⁡ θ + cos 3 ⁡ φ 3 sin ⁡ θ cos ⁡ θ + sin 3 ⁡ φ 3 sin ⁡ θ + cos ⁡ θ 0 π 2 d θ =

E substituindo os limites chegamos nessa coisinha pequenina aqui

16 ∫ 0 π 2 - cos ⁡ π 2 sin �� θ cos ⁡ θ + cos 3 ⁡ π 2 3 sin ⁡ θ cos ⁡ θ + sin 3 ⁡ π 2 3 sin ⁡ θ + cos ⁡ θ - - cos ⁡ 0 sin ⁡ θ cos ⁡ θ + cos 3 ⁡ 0 3 sin ⁡ θ cos ⁡ θ + sin 3 ⁡ 0 3 sin ⁡ θ + cos ⁡ θ d θ =

Mas que simplifica pra isso já que cos ⁡ π 2 = 0 e sin ⁡ π 2 = 1 ...

16 ∫ 0 π 2 1 3 sin ⁡ θ + cos ⁡ θ - - sin ⁡ θ cos ⁡ θ + 1 3 sin ⁡ θ cos ⁡ θ d θ =

16 ∫ 0 π 2 1 3 sin ⁡ θ + cos ⁡ θ + 2 3 sin ⁡ θ cos ⁡ θ d θ =

Integrando de forma semelhante, mas em θ agora...

16 - 1 3 cos ⁡ θ + 1 3 sin ⁡ θ + 2 3 sin 2 ⁡ θ 2 0 π 2 =

16 - 1 3 cos ⁡ π 2 + 1 3 sin ⁡ π 2 + sin 2 ⁡ π 2 3 - - 1 3 cos ⁡ 0 + 1 3 sin ⁡ 0 + sin 2 ⁡ 0 3 =

16 1 3 + 1 3 - - 1 3 = 16 1 =

16

Finalmente, pelo teorema de Stokes...

T r a b a l h o = ∫ C   F → ⋅ d r → = 16

Resposta

16

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê