35) Utilizando o teorema de Stokes, transforme
Em uma integral de linha e calcule:
a) , , com , sendo a normal apontando para cima.
Passo 1
Pelo próprio problema, temos que transformar a integral de superfície em uma integral de linha. Ora! O teorema de Stokes já nos dá essa igualdade:
Agora, para aplicar essa igualdade existem algumas restrições que precisamos ter cuidado:
1º - Uma curva fechada delimitando uma superfície .
2º - Sem singularidades na função Vetorial.
3º - Superfície orientada positivamente.
Vamos passar por cada um deles e verificar se satisfazem ou não 😊!
Passo 2
Bem, a superfície que ele nos deu, já está parametrizada então a gente pode fazer meio que o processo contrário da parametrização para a gente ver que superfície se trata, neh?
Aqui a gente tem que
Como é o cara que depende de e , então...
Eita que chegamos em um cara bem conhecido. Chagamos ao paraboloide:
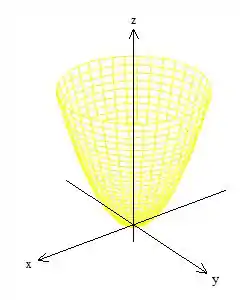
Passo 3
Mas esse cara não é infinito neh? Queremos só um pedacinho dele. Para saber quem é esse pedacinho, analisemos a restrição que o problema nos deu
Ou seja...
Veja bem, é um plano paralelo ao plano ...
Logo, o pedacinho do paraboloide que queremos é esse cara aqui oh, com a borda sendo uma circunferência de raio no plano :
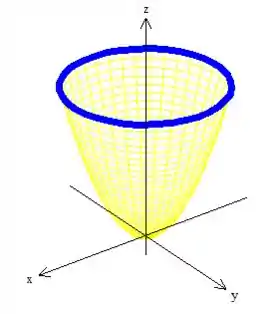
Com isso, agora conhecemos a superfície (o paraboloide) e também a curva que delimita essa superfície (a circunferência). Viu só 😊
Passo 4
As outras duas condições do problema nos pedem que tenhamos:
2º - Sem singularidades na função Vetorial.
Ora, sim! Basta ver o campo
Para você perceber que o campo não tem nenhum bug ou singularidade, como uma divisão por em algum ponto ou algo assim.
3º - Superfície orientada positivamente.
Aqui o que temos que fazer é garantir que o conjunto curva-superfície esteja orientadas positivamente. Pow, como o vetor aponta pra cima
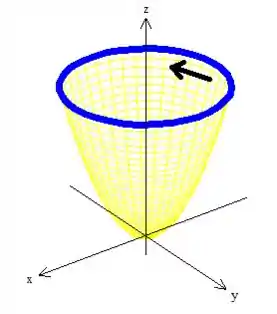
Pela regra da mão direita temos que ter uma cura girando no sentido anti-horário quando vista de cima:
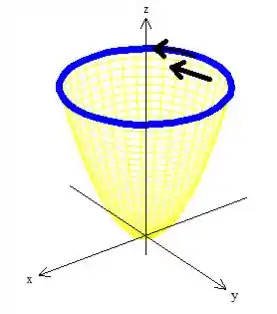
Agora elas estão sim orientadas positivamente, saca?
Passo 5
Com a as três condições de boa, podemos aplicar a igualdade sem problema algum:
Para resolver a integral de linha pelo método direto que conhecemos, façamos:
1º - Parametrizar a curva .
2º - Encontrar .
3º - Encontrar em termos da parametrização.
Passo 6
A curva é uma circunferência de raio que está em cima do plano ...
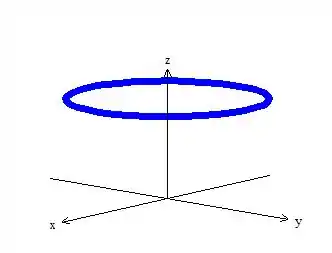
Essa circunferência como vimos tem equação...
Então por semelhança com equação fundamental ...
O da curva é bem conhecido...
Logo a parametrização escrita de uma forma mais elegante é...
Onde dá uma volta completa girando de até , formando a curva redonda completa, saca?
Passo 7
A nossa segunda tarefa é determinar o termo ...
Aqui só tem um detalhe muito importante. Para onde a curva gira com essa parametrização? Ora, essa e uma parametrização clássica onde a curva gira sempre no sentido anti-horário quando vista de cima:
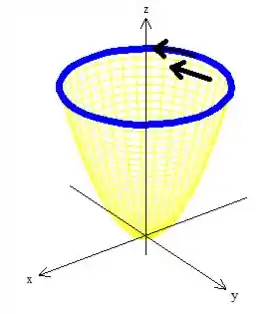
Ai eu te pergunto, é isso que a gente quer? SIM! Então vamos deixar do jeito como está! Se não tivesse, a gente mudaria o sinal da derivada, ok...
Sacou? Fique atento a isso! 😉
Passo 8
Como terceira e última tarefa antes de integrar tudo, só temos que transformar o campo ...
Como ...
Passo 9
Jogando tudo na integral de linha...
Calculando o produto escalar...