39) Calcule
Onde e é a intersecção da superfície , com o plano , orientada no sentido de crescimento de .
Passo 1
Uma integral de linha como essa a gente sabe que tem dois meios basicamente que podemos resolver:
1º - Resolver pelo método diretão.
2º - Resolver pelo teorema de Stokes.
Bem, do modo diretão você pode desconfiar pois temos um campo bem chato e essa complexidade e essa complexidade toda não é um bom sinal. Logo podemos pensar no:
O teorema de Stokes
Passo 2
Tão tá bom sabemos que Stokes pode resolver o problema, mas o que ele fala mesmo? Bem basicamente ele iguala a integral de linha com uma de superfície dessa forma aqui:
Assim, ao invés de termos que calcular uma integral de linha, podemos calcular uma integral de superfície 😉!
Porém Stokes não é só isso! Se não taria muito bom, ne? Para aplicar a igualdade entre as integrais antes devemos averiguar as condições desse Teorema, que nos pede basicamente três coisas:
1º - Uma curva fechada delimitando uma superfície .
2º - Sem singularidades na função Vetorial.
3º - Superfície orientada positivamente.
Vamos passar por cada um deles e verificar se satisfazem ou não 😊!
Passo 3
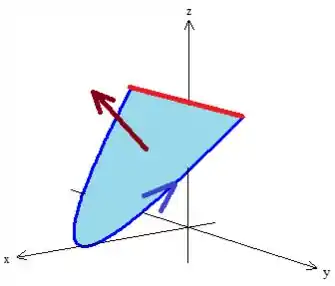
A curva dada no problema é a intersecção do paraboloide . Uma parábola de cabeça pra cima no plano , mas como estamos no espaço são um monte delas ao redor de . Veja:
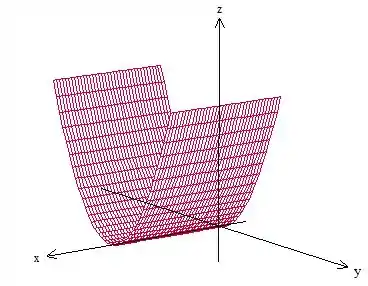
Bem e esse cara está se intercedendo com um plano dessa forma aqui oh
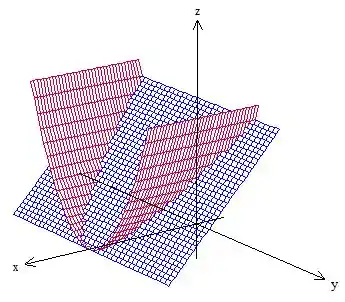
Como queremos apenas a parte onde ... Veja aqui a curva ! Vou destacar ela aqui pra você, oh:
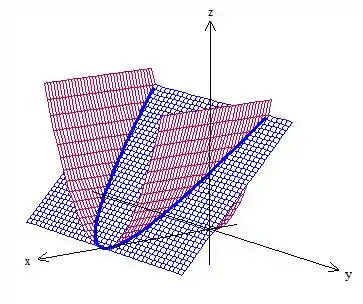
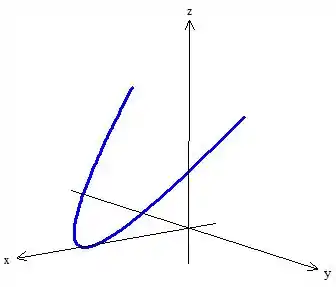
Passo 4
Eita Preula! A curva que encontramos tem um sério problema: ela é aberta e não delimita nenhuma superfície.
Porém nem tudo está perdido 😊! Veja que essa curva se fecha caso colocamos aquela retinha ali na parede ...
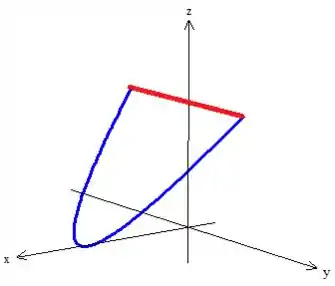
Matematicamente, essa reta tem o e veja que ela tem um constante, pois ela não varia nele. Para descobri-lo, basta pegar o plano e zerar o :
O é o único carinha que varia nessa reta.
Bem, mas agora, com essa retinha adicionada (vamos chamar essa reta de , ok) podemos fechar a superfície no seu interior, onde a mais evidente é o próprio pedacinho de plano 😉!
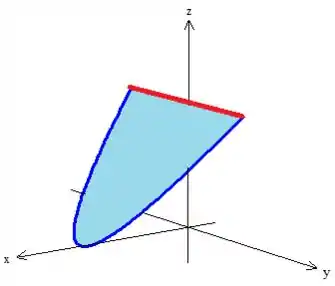
A esse pedacinho, vamos chamar de (apenas nomes para não confundirmos).
Passo 5
A segunda condição de Stokes que precisamos analisar é:
2º - Sem singularidades na função Vetorial.
Ora, sim! Basta ver o campo
Para você perceber que o campo não tem nenhum bug ou singularidade, como uma divisão por em algum ponto ou algo assim.
Passo 6
3º - Superfície orientada positivamente.
Aqui o que temos que fazer é garantir que o conjunto curva-superfície esteja orientadas positivamente. Como a curva azul (original) gira no sentido de maior crescimento de
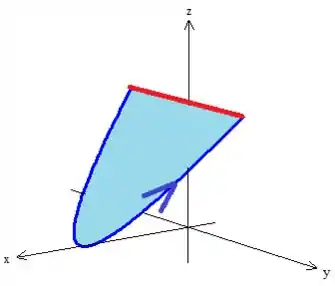
Então pela regra da mão direita a gente tem o vetor normal apontado lá pra cima...
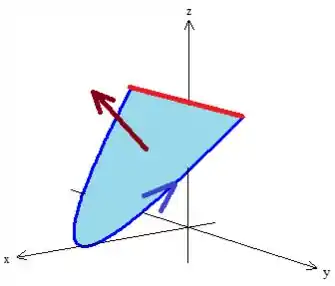
Eis que elas agora sim estão orientadas positivamente, saca? :)
Passo 7
Com as condições averiguadas e sendo satisfeitas, podemos aplicar a igualdade numa nice:
Como a curva é a borda da superf��cie , o que no caso são as curvas e ...
Queremos na real a integral de linha em cima da curva (curva parabólica), então a isolemos...
Eu sei, trocar uma integral por outras duas parece insano, mas vai por mim que isso é o método mais rápido 😐. Bora calcular então 😉?
Passo 8
Começando pela integral de superfície
podemos encontrar esse rotacional numa boa fazendo...
Como
Então...
Para calcular a integral de superfície e fugir da integral de linha, precisamos:
1º - Parametrizar a superfície .
2º - Encontrar o termo .
Bora?
Passo 9
Para parametrizar a superfície saca só: estamos em cima de um plano...
Então podemos parametrizar de forma explícita, pois o é um cara livre (parâmetro) e depende de que também é um cara livre...
Agora esses parâmetros estão variando dentro do pedaço de parábola vista de cima...
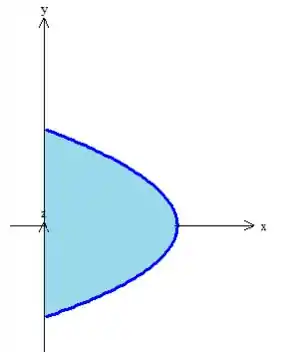
Onde podemos encontrar a equação dessa elipse fazendo a intersecção:
Então o varia de até essa parábola:
Para a char as pontinhas do , é só substituir o na parábola...
Então temos...
Passo 10
Quanto o termo , que é a nossa segunda tarefa na resolução da integral de superfície...
Onde o é fácil de se obter pelo macete de parametrização por gráfico de função ...
Ahhhh! Veja que esse vetor normal atende lá as condições de termos o vetor normal pra cima. Se não atendesse era só inverter o sinal ;D
Então...
Passo 11
Jogando esses dados então na integral de superfície...
Como já temos a região descrita...
Então...
Passo 12
É! Eu sei que o problema é grande, mas não desista agora que estamos quase lá. Nos falta a integral de linha:
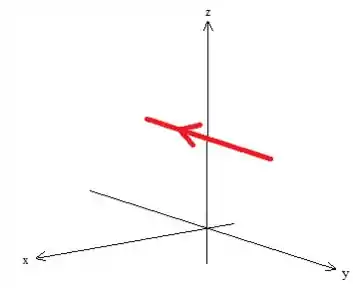
Essa integral está sendo calculada em cima da reta que vimos que tem equação...
E o é o cara que varia. Logo uma Boa parametrização dessa reta é...
Onde , já vimos que vai de até nesse sentido mesmo.
Então o termo ...
O campo é
Mas trocando o e ...
Então na integral de linha isso tudo fica...
Passo 13
Retornando então ao problema inicial de encontrar a integral de linha em cima de indiretamente pelas duas integrais...
Substituindo tudo...