Calcule sendo:

e a parte do hiperbolóide limitada por com normal que aponta para o eixo .

A nossas região pode ser visualizada como

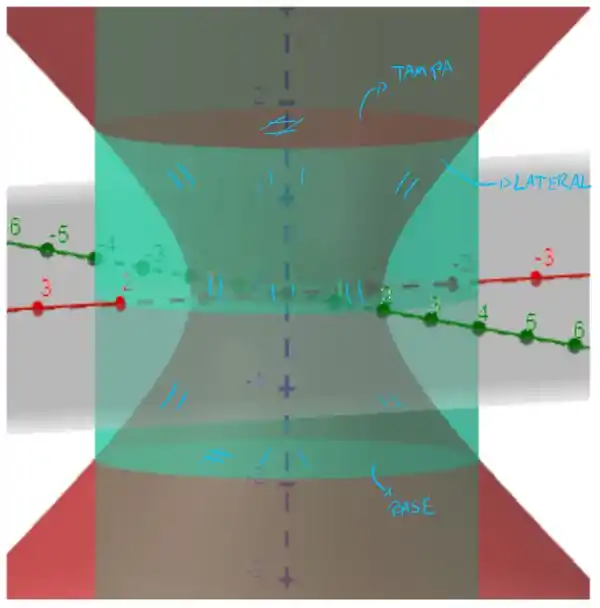
Note que o teorema de Stokes não será útil, não existe uma curva que seja fronteira de nossa superfície. No entanto, a nossa superfície é a lateral de um sólido , que tem como base e tampa dois planos. Então, podemos considerar o teorema da divergência de Gauss, usando um da forma

que é fronteira de , e portanto, a nossa integral pode ser identificada como

Pode não parecer, mas isso facilita muito a nossa vida! Vem comigo!

O lado direito desta expressão tem como integrando a relação

a divergência de qualquer rotacional é sempre nula, portanto, temos que

e, a nossa integral é resumida à

Ou seja, a integral de superfície que queremos é dada por

Vamos tentar expandir o lado direito da expressão acima verificando quem são e . Bora lá!

Temos que a base e a tampa são planos obtidos através da intersecção do hiperbolóide com o cilindro, portanto, temos da equação do hiperbolóide que

mas, o cilindro nos diz que , portanto, obtemos

desta maneira, os dois planos são simplesmente

E, quem são os vetores normais a estes planos? Note que o enunciado nos indica que o vetor normal da superfície aponta para o eixo , portanto, estamos considerando a normal interior ao sólido. De forma, que nas tampas temos as normais

e

Vamos usar isso para resolver a nossa integração! Saca só!

Nós temos que calcular

Como temos que

A integral acima se torna

e, uma vez que a região delimitada pelo cilindro é a mesma em e , temos que as integrais são numericamente iguais, e sendo assim

A questão foi isso! Te vejo na próxima! Tchau Tchau!